练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设D表示不等式组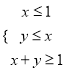所确定的平面区域，在D内存在 无数个点落在y＝a（x+2）上，则a的取值范围是 （　　）

    A. R B. （，1） C. （0， ） D. （﹣∞，0]∪[，+∞）

    【答案】C

    【解析】

    作出约束条件不等式组所对应的可行域（如图阴影）直线表示过点且斜率为的直线，联立可解得，由斜率公式可得，结合图象可得要使直线与内存在无数个点落在上， ，故选C.

    【方法点晴】本题主要考查线性规划中利用可行域求目标函数的最值，属简单题.求目标函数最值的一般步骤是“一画、二找、三求”：（1）作出可行域（一定要注意是实线还是虚线）；（2）找到目标函数对应的最优解对应点（在可行域内平移变形后的目标函数，最先通过或最后通过的顶点就是最优解）；（3）将最优解坐标代入目标函数求出最值或范围.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知O点为坐标原点，且点A（1，0），B（0，1），C（2sinθ，cosθ）
    （1）若 ，求tanθ的值；
    （2）若 =1，求sinθcosθ的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设p：实数x满足x2﹣4ax+3a2＜0，其中a＜0，q：实数x满足x2﹣x﹣6≤0或x2+2x﹣8＞0，且非p是非q的必要不充分条件，则实数a的范围是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在直角坐标系中，直线的倾斜角为且经过点，以原点为极点，以轴正半轴为极轴，与直角坐标系取相同的长度单位，建立极坐标系，设曲线的极坐标方程为.

    （1）若直线与曲线有公共点，求的取值范围；

    （2）设为曲线上任意一点，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知关于x的函数 ．
    （1）如果函数 ，求b、c；
    （2）设当x∈（ ，3）时，函数y=f（x）﹣c（x+b）的图象上任一点P处的切线斜率为k，若k≤2，求实数b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】广东某市一玩具厂生产一种玩具深受大家喜欢，经市场调查该商品每月的销售量（单位：千件）与销售价格（单位：元/件）满足关系式，其中， 为常数．已知销售价格为4元/件时，每日可售出玩具21千件．

    （1）求的值；

    （2）假设该厂生产这种玩具的成本、员工工资等所有开销折合为每件2元（只考虑销售出的件数），试确定销售价格的值，使该厂每日销售这种玩具所获得的利润最大．（保留1位小数）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知△ABC的顶点A（5，1），AB边上的中线CM所在直线方程为2x﹣y﹣5=0，∠B的平分线BN所在直线方程为x﹣2y﹣5=0．求：
    （1）顶点B的坐标；
    （2）直线BC的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在平面直角坐标系中，直线的参数方程是（为参数），以为极点， 轴的正半轴为极轴，建立极坐标系，曲线的极坐标方程为，且直线与曲线交于两点.

    （Ⅰ）求曲线的直角坐标方程及直线恒过的定点的坐标；

    （Ⅱ）在（Ⅰ）的条件下，若，求直线的普通方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司有4家直营店， ， ， ，现需将6箱货物运送至直营店进行销售，各直营店出售该货物以往所得利润统计如下表所示．根据此表，该公司获得最大总利润的运送方式有

    A. 种 B. 种 C. 种 D. 种

    查看答案和解析>>

    同步练习册答案