练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设p：实数x满足x2﹣4ax+3a2＜0，其中a＜0，q：实数x满足x2﹣x﹣6≤0或x2+2x﹣8＞0，且非p是非q的必要不充分条件，则实数a的范围是 ．

    【答案】[﹣ ，0）∪（﹣∞，﹣4]
    【解析】解：对于命题p：由x2﹣4ax+3a2＜0及a＜0，得3a＜x＜a，即p：3a＜x＜a． 对于命题q：又由x2﹣x﹣6≤0，得﹣2≤x≤3，由x2+2x﹣8＞0，得x＜﹣4或x＞2，
    那么q：x＜﹣4或x≥﹣2．
    由于，非p是非q的必要不充分条件，即非q非p，且非p推不出非q，
    等价于pq且q推不出p，
    于是，得 或 ，
    解得﹣ ≤a＜0或a≤﹣4，
    故所求a的范围为[﹣ ，0）∪（﹣∞，﹣4]．
    所以答案是：[﹣ ，0）∪（﹣∞，﹣4]．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】若向量 ， ，且 ，若 ，则β﹣α的值为（ ）
    A. 或
    B.
    C.
    D. 或

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某篮球队与其他6支篮球队依次进行6场比赛，每场均决出胜负，设这支篮球队与其他篮球队比赛中获胜的事件是独立的，并且获胜的概率均为 ．
    （1）求这支篮球队首次获胜前已经负了两场的概率；
    （2）求这支篮球队在6场比赛中恰好获胜3场的概率；
    （3）求这支篮球队在6场比赛中获胜场数的期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥S﹣ABCD中，底面ABCD为正方形，△SAD是正三角形，P，Q分别是棱SC，AB的中点，且平面SAD⊥平面ABCD．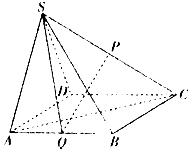
    （1）求证：PQ∥平面SAD；
    （2）求证：SQ⊥AC．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    (1)求曲线在点处的切线方程；(2)求函数在上的最大值；

    (3)求证：存在唯一的，使得.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列满足， ，（ N*）.

    （Ⅰ）写出的值；

    （Ⅱ）设，求的通项公式；

    （Ⅲ）记数列的前项和为，求数列的前项和的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】有以下命题：
    ①若f（x）=x3+（a﹣1）x2+3x+1没有极值点，则﹣2＜a＜4；
    ②集合M={1，2，zi}，i为虚数单位，N={3，4}，M∩N={4}，则复数z=﹣4i；
    ③若函数f（x）= ﹣m有两个零点，则m＜ ．
    其中正确的是 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设D表示不等式组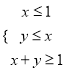所确定的平面区域，在D内存在 无数个点落在y＝a（x+2）上，则a的取值范围是 （　　）

    A. R B. （，1） C. （0， ） D. （﹣∞，0]∪[，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】过抛物线的焦点的直线交抛物线于， 两点， 为坐标原点，若，则△的面积为（ ）

    A. B. C. D.

    查看答案和解析>>

    同步练习册答案