
分析 (1)由点P满足$\overrightarrow{CP}$=λ$\overrightarrow{CA′}$+(1-λ)得即点P在直线EA′上,所以CP?面CEA′.只需证DB⊥面CEA′,即可得BD⊥CP.
(2)当λ=$\frac{1}{2}$时,P为线段EA′DE中点,由(1)可知∠A′EC为二面角A′-BD-C的平面角,得∠A′EC=120°过A′作垂直直线CE的直线,垂足为O,以O为原点,OC为x轴,OA′为z轴,建立空间直角坐标系,设BC=2.则B($\frac{\sqrt{3}}{2},-1,0)$,C($\frac{3\sqrt{3}}{2},0,0$),D($\frac{\sqrt{3}}{2}$,1,0),A′(0,0,$\frac{3}{2}$),E($\frac{\sqrt{3}}{2},0,0$).故P($\frac{\sqrt{3}}{4},0,\frac{3}{4}$),利用向量法求解.
解答 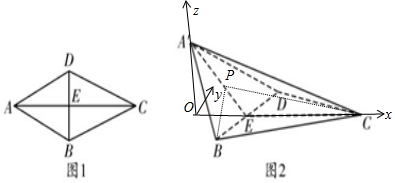 解(1)∵点P满足$\overrightarrow{CP}$=λ$\overrightarrow{CA′}$+(1-λ)∴$\overrightarrow{CE}$,$\overrightarrow{EP}=λ\overrightarrow{E{A}^{′}}$,即点P在直线EA′上,所以CP?面CEA′.
解(1)∵点P满足$\overrightarrow{CP}$=λ$\overrightarrow{CA′}$+(1-λ)∴$\overrightarrow{CE}$,$\overrightarrow{EP}=λ\overrightarrow{E{A}^{′}}$,即点P在直线EA′上,所以CP?面CEA′.
在△A′BD中,A′E⊥DB,在△CBD中,CE⊥DB,
∴DB⊥面CEA′,∴BD⊥CP.
(2)当λ=$\frac{1}{2}$时,P为线段EA′DE中点,
由(1)可知∠A′EC为二面角A′-BD-C的平面角,∴∠A′EC=120°
过A′作垂直直线CE的直线,垂足为O,以O为原点,OC为x轴,OA′为z轴,
建立空间直角坐标系,设BC=2.
则B($\frac{\sqrt{3}}{2},-1,0)$,C($\frac{3\sqrt{3}}{2},0,0$),D($\frac{\sqrt{3}}{2}$,1,0),A′(0,0,$\frac{3}{2}$),E($\frac{\sqrt{3}}{2},0,0$).
故P($\frac{\sqrt{3}}{4},0,\frac{3}{4}$),$\overrightarrow{BP}=(-\frac{\sqrt{3}}{4},1,\frac{3}{4}$),$\overrightarrow{BC}=(\sqrt{3},-1,0)$,$\overrightarrow{A′C}=(\frac{3\sqrt{3}}{2},0,-\frac{3}{2}$)
设面A′CD的法向量为$\overrightarrow{n}=(x,y,z)$
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{DC}=\sqrt{3}x-y=0}\\{\overrightarrow{n}•\overrightarrow{A′C}=\frac{3\sqrt{3}}{2}x-\frac{3}{2}z=0}\end{array}\right.$,可取$\overrightarrow{n}=(1,\sqrt{3},\sqrt{3})$.
cos<$\overrightarrow{n},\overrightarrow{BP}$>=$\frac{3\sqrt{3}}{7}$,
∴直线BP与平面A′CD所成角的正弦值为$\frac{3\sqrt{3}}{7}$.
点评 本题考查了空间线线垂直的判定,向量法求解线面角,属于中档题.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin(2x+$\frac{π}{6}$) | B. | y=sin2x | C. | y=sin(2x+$\frac{π}{3}$) | D. | y=sin(2x-$\frac{π}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{π}$ | B. | $\frac{4}{π}$ | C. | $\frac{2}{{π}^{3}}$ | D. | $\frac{4}{{π}^{3}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com