练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．直线y=4x与曲线y=x2围成的封闭区域面积为$\frac{32}{3}$．

    分析 联立方程组求出两曲线的交点坐标，根据定积分的几何意义求出面积．

    解答 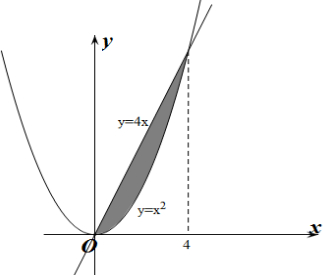解：联立方程组$\left\{\begin{array}{l}{y=4x}\\{y={x}^{2}}\end{array}\right.$，解得$\left\{\begin{array}{l}{x=0}\\{y=0}\end{array}\right.$或$\left\{\begin{array}{l}{x=4}\\{y=16}\end{array}\right.$，
    ∴S=${∫}_{0}^{4}$（4x-x2）dx=（2x2-$\frac{{x}^{3}}{3}$）${|}_{0}^{4}$=$\frac{32}{3}$．
    故答案为$\frac{32}{3}$．

    点评 本题考查了定积分的应用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

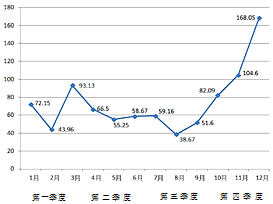    2．北京市2016年12个月的PM2.5平均浓度指数如图所示．由图判断，四个季度中PM2.5的平均浓度指数方差最小的是（　　）
    A．第一季度B．第二季度C．第三季度D．第四季度

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．已知双曲线x2+ny2=1（n∈R）与椭圆$\frac{x^2}{6}+\frac{y^2}{2}=1$有相同的焦点，则该双曲线的渐近线方程为y=±$\sqrt{3}$x．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知数列{an}的通项公式为an=$\frac{n•{3}^{n}}{{3}^{n}-1}$（n≥1，n∈N*）．
    （Ⅰ）求a1，a2，a3的值；
    （Ⅱ）求证：对任意的自然数n∈N*，不等式a1•a2…an＜2•n!成立．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知等比数列{an}中，a3a9=2a52，且a3=2，则a5=（　　）
    A．-4B．4C．-2D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    17．如图1，菱形ABCD的对角线AC与BD交于点E，∠BAD=60°，将△BAD折起，使得点A到点A′的位置，点P满足$\overrightarrow{CP}$=λ$\overrightarrow{CA′}$+（1-λ）$\overrightarrow{CE}$．

    （1）证明：BD⊥CP；
    （2）若λ=$\frac{1}{2}$，二面角A′-BD-C为120°，求直线BP与平面A′CD所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知等差数列{an}中，a2=2，a12=-2，则{an}的前10项和为6．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    1．已知函数f（x）=$\frac{m}{x}$+xlnx（m＞0），g（x）=lnx-2．
    （1）当m=1时，求函数f（x）的单调区间；
    （2）设函数h（x）=f（x）-xg（x）-$\sqrt{2}$，x＞0．若函数y=h（h（x））的最小值是$\frac{3\sqrt{2}}{2}$，求m的值；
    （3）若函数f（x），g（x）的定义域都是[1，e]，对于函数f（x）的图象上的任意一点A，在函数g（x）的图象上都存在一点B，使得OA⊥OB，其中e是自然对数的底数，O为坐标原点，求m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．二项式（$\frac{\sqrt{x}}{2}$-$\frac{2}{x}$）10的展开式中，$\sqrt{x}$项的系数是（　　）
    A．$\frac{15}{2}$B．-$\frac{15}{2}$C．15D．-15

    查看答案和解析>>

    同步练习册答案