练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知f（x）=log （x2﹣2x）的单调递增区间是（ ）
    A.（1，+∞）
    B.（2，+∞）
    C.（﹣∞，0）
    D.（﹣∞，1）

    【答案】C
    【解析】解：令t=x2﹣2x＞0，求得x＜0，或x＞2，故函数的定义域为（﹣∞，0）∪（2，+∞），且f（x）=log （x2﹣2x）=g（t）=log t．
    根据复合函数的单调性，本题即求函数t=x2﹣2x在定义域内的减区间．
    再利用二次函数的性质可得函数t=x2﹣2x在定义域内的减区间为（﹣∞，0），
    故选：C．
    令t=x2﹣2x＞0，求得函数的定义域，且f（x）=g（t）=log t，根据复合函数的单调性，本题即求函数t=x2﹣2x在定义域内的减区间，利用二次函数的性质可得函数t=x2﹣2x在定义域内的减区间．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】超市某种绿色食品，过去20个月该食品的月市场需求量（单位： ， ）即每月销售的数据记录如下：

    137 108 114 121 115 135 122 140 128 139

    125 140 130 125 105 115 133 124 149 115

    对这20个数据按组距10进行分组，并统计整理，绘制了如下尚不完整的统计图表：

    （Ⅰ）写出， 的值.若视分布在各区间内的频率为相应的概率，试计算；

    （Ⅱ）记组月市场需求量数据的平均数与方差分别为， ， 组月市场需求量数据的平均数与方差分别为， ，试分别比较与， 与的大小；（只需写出结论）

    （Ⅲ）为保证该绿色产品的质量，超市规定该产品仅在每月一日上架销售，每月最后一日对所有未售出的产品进行下架处理.若超市每售出该绿色食品可获利润5元，未售出的食品每亏损3元，并且超市为下一个月采购了该绿色食品，求超市下一个月销售该绿色食品的利润的分布列及数学期望.（以分组的区间中点值代表该组的各个值，并以月市场需求量落入该区间的频率作为月市场需求量取该组区间中点值的概率）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥中， ， ， ，平面平面， 为等腰直角三角形，

    （1）证明： 为直角三角形；

    （2）若四棱锥的体积为，求的面积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，ABCD是正方形，PD⊥平面ABCD，PD=AB=2，E，F，G分别是PC，PD，BC的中点．

    （1）求证：平面PAB∥平面EFG；
    （2）在线段PB上确定一点Q，使PC⊥平面ADQ，并给出证明；
    （3）求出D到平面EFG的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥P﹣ABC中，PA⊥平面ABC，AC⊥BC，D为侧棱PC的中点，它的正（主）视图和侧（左）视图如图所示．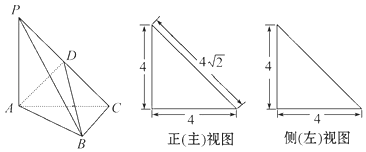

    （Ⅰ）求三棱锥P﹣ABD的体积．
    （Ⅱ）在∠ACB的平分线所在直线上确定一点Q，使得PQ∥平面ABD，并求此时PQ的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在正三棱柱ABC﹣A1B1C1中，已知AB=CC1=2，则异面直线AB1和BC1所成角的余弦值为（ ）
    A.0
    B.
    C.﹣
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数.

    （I）函数在点处的切线与直线垂直，求a的值；

    （II）讨论函数的单调性；

    （III）不等式在区间上恒成立，求实数a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】现有一个关于平面图形的命题：如图，同一个平面内有两个边长都是a的正方形，其中一个的某顶点在另一个的中心，则这两个正方形重叠部分的面积恒为 ．类比到空间，有两个棱长均为a的正方体，其中一个的某顶点在另一个的中心，则这两个正方体重叠部分的体积恒为 ．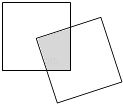

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比，收获时各随机抽取了100个网箱，测量各箱水产品的产量（单位：kg）其频率分布直方图如下：

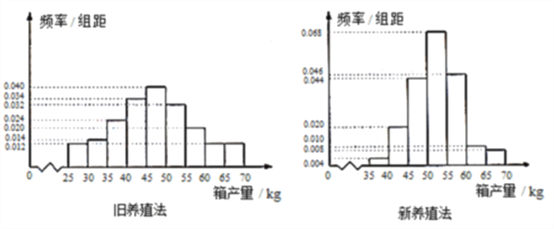
    （1） 记表示事件“旧养殖法的箱产量低于50kg”，估计的概率；

    （2）填写下面联表，并根据列联表判断是否有％的把握认为箱产量与养殖方法有关：

    箱产量

    箱产量

    旧养殖法

    新养殖法

    （3）根据箱产量的频率分布直方图，对两种养殖方法的优劣进行比较.

    附：

    0.050

    0.010

    0.001

    3.841

    6.635

    10.828

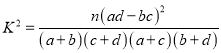
    查看答案和解析>>

    同步练习册答案