
(本小题满分14分)
某家电生产企业根据市场调查分析,决定调整新产品生产方案,准备每周(按40个工时计算)生产空调器、彩电、冰箱共120台,且冰箱至少生产20台. 已知生产这些家电产品每台所需工时和每台产值如下表:
家电名称 | 空调器 | 彩电 | 冰箱 |
工 时 |
|
|
|
产值/千元 | 4 | 3 | 2 |
问每周应生产空调器、彩电、冰箱各多少台,才能使产值最高?最高产值是多少?(以千元为单位)
每周应生产空调器10台,彩电90台,冰箱20台,才能使产值最高,最高产值是350千元
【解析】
试题分析:(1)含有实际背景的线性规划问题其解题关键是找到制约求解目标的两个变量,用这两个变量建立可行域和目标函数,解题时要注意题目中的各种制约的关系,列出全面的制约条件和正确的目标函数;(2)平面区域的画法:线定界、点定线(注意实虚线);(3)求最值:求二元一次函数 的最值,将函数
的最值,将函数 转化为直线的点斜式
转化为直线的点斜式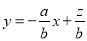 ,通过求直线的截距
,通过求直线的截距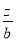 的最值间接求出
的最值间接求出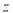 的最值,最优解在顶点或边界取得.
的最值,最优解在顶点或边界取得.
试题解析:【解析】
设每周生产空调器x台、彩电y台,则生产冰箱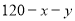 台,产值为z千元,
台,产值为z千元,
则依题意得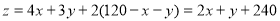 , (4分)
, (4分)
且x,y满足 即
即 (8分)
(8分)
可行域如图所示. (10分)
解方程组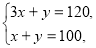 得
得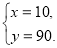 即M(10,90).(11分)
即M(10,90).(11分)
让目标函数表示的直线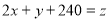 在可行域上平移,
在可行域上平移,
可得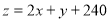 在M(10,90)处取得最大值,且
在M(10,90)处取得最大值,且
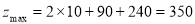 (千元). (13分)
(千元). (13分)
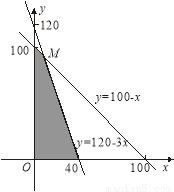
答:每周应生产空调器10台,彩电90台,冰箱20台,才能使产值最高,最高产值是350千元.(14分)
考点:线性规划的应用.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源:2014-2015学年河北邢台一中高二上学期期中考试文科数学试卷(解析版) 题型:选择题
已知抛物线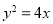 ,以
,以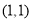 为中点作抛物线的弦,则这条弦所在直线的方程为( )
为中点作抛物线的弦,则这条弦所在直线的方程为( )
A.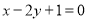 B.
B.
C.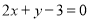 D.
D.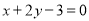
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省山一等七校高三12月联考理科数学试卷(解析版) 题型:选择题
已知双曲线的中心在原点,一个焦点为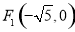 ,点
,点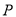 在双曲线上,且线段
在双曲线上,且线段 的中点坐标为
的中点坐标为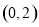 ,则此双曲线的方程是( )
,则此双曲线的方程是( )
A.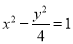 B.
B.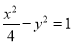 C.
C.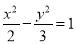 D.
D.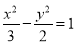
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省肇庆市毕业班第一次统一检测文科数学试卷(解析版) 题型:选择题
设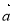 ,
,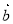 为非零向量,
为非零向量,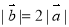 ,两组向量
,两组向量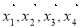 和
和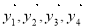 均由2个
均由2个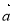 和2个
和2个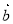 排列而成. 若
排列而成. 若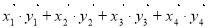 所有可能取值中的最小值为
所有可能取值中的最小值为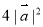 ,则
,则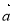 与
与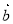 的夹角为
的夹角为
A.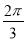 B.
B.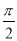 C.
C.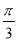 D.
D.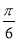
查看答案和解析>>
科目:高中数学 来源:2014-2015学年广东省肇庆市毕业班第一次统一检测理科数学试卷(解析版) 题型:选择题
一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该几何体的外接球的表面积为

A.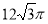 B.
B.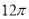 C.
C.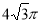 D.
D.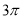
查看答案和解析>>
科目:高中数学 来源:2014-2015学年福建省四地六校高三上学期第三次月考文科数学试卷(解析版) 题型:选择题
若某几何体的三视图如图所示,则这个几何体的体积是( )
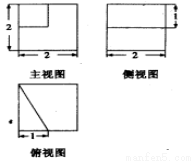
A.5 B.6 C.7 D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com