
已知集合A={x|x2-2x-3≤0},B={x|x2-2mx+m2-4≤0,x∈R,m∈R}.
(1) 当m=2时,求A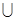 B;
B;
(2) 若A∩B=[1,3],求实数m的值;
(3) 若A⊆∁RB,求实数m的取值范围.
(1) A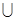 B="{x|-1≤x≤4}" (2) m=3 (3) {m|m>5,或m<-3}
B="{x|-1≤x≤4}" (2) m=3 (3) {m|m>5,或m<-3}
解析试题分析:(1) 当m=2时,B={x|0≤x≤4}.1分
∴A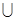 B={x|-1≤x≤4}3分
B={x|-1≤x≤4}3分
(2) 由已知得A={x|-1≤x≤3},B={x|m-2≤x≤m+2}.5分
∵A∩B=[1,3],∴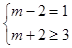
 7分
7分
∴m=3. 8分
(3)∁RB={x|x<m-2或x>m+2},10分
∵A⊆∁RB,∴m-2>3或m+2<-1,即m>5或m<-3. 12分
所以实数m的取值范围是{m|m>5,或m<-3}.14分
考点:集合的交并补运算即包含关系
点评:集合运算题常借助于数轴,将已知中的集合标注在数轴上,使其满足相应的包含关系,进而确定集合边界值的满足的条件


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:解答题
从集合 中任取三个元素构成三元有序数组
中任取三个元素构成三元有序数组 ,规定
,规定 .
.
(1)从所有的三元有序数组中任选一个,求它的所有元素之和等于10的概率
(2)定义三元有序数组 的“项标距离”为
的“项标距离”为 (其中
(其中 ),从所有的三元有序数组中任选一个,求它的“项标距离”d为偶数的概率.
),从所有的三元有序数组中任选一个,求它的“项标距离”d为偶数的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题12分)已知集合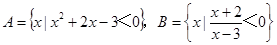
(Ⅰ)在区间(-4,4)上任取一个实数x,求“x∈A∩B”的概率;
(Ⅱ)设(a,b)为有序实数对,其中a是从集合A中任取的一个整数,b是从集合B中任取的一个整数,求“b-a∈A∪B”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com