
【题目】已知数列![]() 的各项均为正数,记数列
的各项均为正数,记数列![]() 的前n项和为
的前n项和为![]() ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,且
,且![]() .
.
(1)求![]() 的值;
的值;
(2)求数列![]() 的通项公式;
的通项公式;
(3)若![]() ,且
,且![]() 成等比数列,求k和t的值.
成等比数列,求k和t的值.
【答案】(1)1(2)![]() .(3)
.(3)![]() .
.
【解析】
(1)令![]() 代入递推关系,即可求得
代入递推关系,即可求得![]() 的值;
的值;
(2)连续两次利用“临差法”,即多递推一项再相减,从而构造出![]() 这一递推关系,再利用等比数列通项公式,即可得答案;
这一递推关系,再利用等比数列通项公式,即可得答案;
(3)由(2)可知![]() ,由
,由![]() 成等比数列,可得
成等比数列,可得![]() ,即
,即![]() ,再根据等式两边奇、偶数的特点,推理得到k和t的值.
,再根据等式两边奇、偶数的特点,推理得到k和t的值.
(1)由![]() ,得
,得![]() ,即
,即![]() .
.
因为![]() ,所以
,所以![]() .
.
(2)因为![]() ,①
,①
所以![]() ,②
,②
②-①,得![]() .
.
因为![]() ,
,
所以![]() ,③
,③
所以![]() ,④
,④
④-③,得![]() ,即
,即![]() ,
,
所以当![]() 时,
时,![]() .
.
又由![]() ,得
,得![]() ,
,
即![]() .
.
因为![]() ,所以
,所以![]() ,所以
,所以![]() ,所以对
,所以对![]() ,都有
,都有![]() 成立,
成立,
所以数列![]() 的通项公式为
的通项公式为![]() .
.
(3)由(2)可知![]() .
.
因为![]() 成等比数列,
成等比数列,
所以![]() ,即
,即![]() ,
,
所以![]() ,即
,即![]() .
.
由于![]() ,所以
,所以![]() ,即
,即![]() .
.
当![]() 时,
时,![]() ,得
,得![]() .
.
当![]() 时,由
时,由![]() ,得
,得![]() 为奇数,
为奇数,
所以![]() ,即
,即![]() ,代入(*)得
,代入(*)得![]() ,即
,即![]() ,此时k无正整数解.
,此时k无正整数解.
综上,![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】某校高三(1)班在一次语文测试结束后,发现同学们在背诵内容方面失分较为严重.为了提升背诵效果,班主任倡议大家在早、晚读时间站起来大声诵读,为了解同学们对站起来大声诵读的态度,对全班50名同学进行调查,将调查结果进行整理后制成下表:
考试分数 |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 5 | 10 | 5 |
赞成人数 | 4 | 6 | 9 | 3 | 6 | 4 |
(1)欲使测试优秀率为30%,则优秀分数线应定为多少分?
(2)依据第1问的结果及样本数据研究是否赞成站起来大声诵读的态度与考试成绩是否优秀的关系,列出2×2列联表,并判断是否有90%的把握认为赞成与否的态度与成绩是否优秀有关系.
参考公式及数据: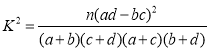 ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦点为
的焦点为![]() ,
,![]() ,离心率为
,离心率为![]() ,点P为椭圆C上一动点,且
,点P为椭圆C上一动点,且![]() 的面积最大值为
的面积最大值为![]() ,O为坐标原点.
,O为坐标原点.
(1)求椭圆C的方程;
(2)设点![]() ,
,![]() 为椭圆C上的两个动点,当
为椭圆C上的两个动点,当![]() 为多少时,点O到直线MN的距离为定值.
为多少时,点O到直线MN的距离为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,焦距为2,且经过点
,焦距为2,且经过点![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 经过点
经过点![]() ,与椭圆
,与椭圆![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)在![]() 轴上是否存在点
轴上是否存在点![]() ,使得以
,使得以![]() ,
,![]() 为邻边的平行四边形是菱形?如果存在,求出
为邻边的平行四边形是菱形?如果存在,求出![]() 的取值范围,如果不存在,请说明理由.
的取值范围,如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 与曲线
与曲线![]() ,(
,(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)写出曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)在极坐标系中,已知![]() 与
与![]() ,
,![]() 的公共点分别为
的公共点分别为![]() ,
,![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与抛物线
与抛物线![]() :
:![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() 的面积为16(
的面积为16(![]() 为坐标原点).
为坐标原点).
(1)求![]() 的方程;
的方程;
(2)直线![]() 经过
经过![]() 的焦点
的焦点![]() 且
且![]() 不与
不与![]() 轴垂直,与
轴垂直,与![]() 交于
交于![]() ,
,![]() 两点,若线段
两点,若线段![]() 的垂直平分线与
的垂直平分线与![]() 轴交于点
轴交于点![]() ,证明:
,证明:![]() 为定值.
为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com