Question

【题目】如图，圆： ．

（1）若圆与轴相切，求圆的方程；

（2）求圆心的轨迹方程；

（3）已知，圆与轴相交于两点（点在点的左侧）．过点任作一条直线与圆： 相交于两点．问：是否存在实数，使得？若存在，求出实数的值，若不存在，请说明理由．

Answer 1

【答案】（1）；（2）（3）存在，使得

【解析】试题分析： 在圆的方程中，令，可得关于的一元二次方程的判别式等于零，由此求得的值，从而求得所求圆的方程。

(2)消去圆心坐标中的参数即可先求出，假设存在实数，当直线直线与轴不垂直时，设直线的方程为，代入，利用韦达定理，根据的斜率之和等于零求得的值，经过检验，当直线与轴垂直时，这个值仍然满足从而得出结论

解析：（1）由圆与轴相切，可知圆心的纵坐标的绝对值与半径相等.故先将圆的方程化成标准方程为： ，由求得.即可得到所求圆的方程为： ；

（2）求圆心点坐标为，则 圆心点的轨迹方程为

（3）令，得，即所以

假设存在实数，当直线AB与轴不垂直时，设直线AB的方程为，

代入得， ，设从而

因为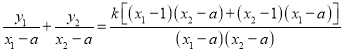

而

因为，所以，即，得．

当直线AB与轴垂直时，也成立．故存在，使得