
分析 由劣弧所对的圆心角最小弦长最短,及过圆内一点最短的弦与过该点的直径垂直,易得到解题思路.
解答 解:由题意,点P(1,$\sqrt{2}$)在圆(x-2)2+y2=8的内部,
圆心为C(2,0),要使得劣弧所对的圆心角最小,只能是直线l⊥CP,
所以k=-$\frac{2-1}{0-\sqrt{2}}$=$\frac{{\sqrt{2}}}{2}$,
故答案为$\frac{{\sqrt{2}}}{2}$.
点评 垂径定理及其推论是解决直线与圆关系时常用的定理,要求大家熟练掌握,垂径定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧.相关推论,过圆内一点垂直于该点直径的弦最短,且弦所在的劣弧最短,优弧最长,弦所对的圆心角、圆周角最小.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
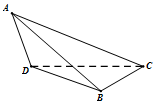 如图,在三棱锥A-BCD中,△ABD为边长等于$\sqrt{2}$正三角形,CD=CB=1.△ADC与△ABC是有公共斜边AC的全等的直角三角形.
如图,在三棱锥A-BCD中,△ABD为边长等于$\sqrt{2}$正三角形,CD=CB=1.△ADC与△ABC是有公共斜边AC的全等的直角三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 四棱锥P-ABCD的三视图如图所示,其五个顶点都在同一球面上,若四棱锥P-ABCD的侧面积等于4(1+$\sqrt{2}$),则该外接球的表面积是( )
四棱锥P-ABCD的三视图如图所示,其五个顶点都在同一球面上,若四棱锥P-ABCD的侧面积等于4(1+$\sqrt{2}$),则该外接球的表面积是( )| A. | 4π | B. | 12π | C. | 24π | D. | 36π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com