
分析 (Ⅰ)通过讨论x的范围得到关于x的不等式组,解出即可;
(Ⅱ)根据绝对值的性质求出f(x)的最小值,问题转化为|a-1|>f(x)min,求出a的范围即可.
解答 解:(Ⅰ)f(x)=|x+1|+|x-1|<4
?$\left\{\begin{array}{l}x≤-1\\-x-1-x+1<4\end{array}\right.$或$\left\{\begin{array}{l}-1<x≤1\\ x+1-x+1<4\end{array}\right.$或$\left\{\begin{array}{l}x>1\\ x+1+x-1<4\end{array}\right.$,
解得:-2<x≤-1或-1<x≤1或1<x<2,
故不等式的解集为(-2,2); …(5分)
(Ⅱ)∵f(x)=|x+1|+|x-1|≥|(x+1)-(x-1)|=2,
∴f(x)min=2,当且仅当(x+1)(x-1)≤0时取等号,
而不等式f(x)-|a-1|<0有解?|a-1|>f(x)min=2,
又|a-1|>2?a-1<-2或a-1>2
故a的取值范围是(-∞,-1)∪(3,+∞). …(10分)
点评 本题考查了解绝对值不等式问题,考查分类讨论思想,是一道中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
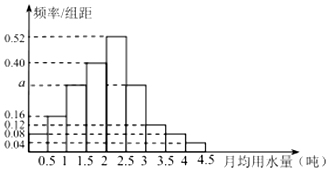 我国上是世界严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过x的部分按平价收费,超过x的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
我国上是世界严重缺水的国家,城市缺水问题较为突出,某市政府为了鼓励居民节约用水,计划在本市试行居民生活用水定额管理,即确定一个合理的居民月用水量标准x(吨),用水量不超过x的部分按平价收费,超过x的部分按议价收费,为了了解全市民月用水量的分布情况,通过抽样,获得了100位居民某年的月用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1±$\sqrt{10}$ | B. | 1$±\sqrt{10}$ | C. | -1-$\sqrt{10}$ | D. | 1-$\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
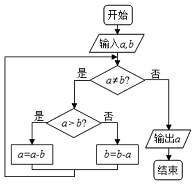 下面程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为8,12,则输出的a=( )
下面程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为8,12,则输出的a=( )| A. | 2 | B. | 0 | C. | 4 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com