
分析 推导出EF∥平面BCC1,过EF且过B的平面与面BCC1的交线l平行于EF,l即为BC1.由此能求出过点B,E,F的平面截该正方体所得的截面面积S.
解答 解:∵正方体ABCD-A1B1C1D1中,E、F分别是棱AD、DD1的中点,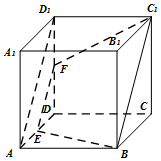
∴EF∥AD1∥BC1,
∵EF?平面BCC1,BC1?平面BCC1,
∴EF∥平面BCC1,
由线面平行性质定理,过EF且过B的平面与面BCC1的交线l平行于EF,l即为BC1.
由正方体的边长为4,可得BE=C1F=$\sqrt{20}$,BC1=2EF=4$\sqrt{2}$,
截面是等腰梯形,其高为3$\sqrt{2}$,
其面积S=$\frac{(EF+B{C}_{1})}{2}$h=$\frac{2\sqrt{2}+4\sqrt{2}}{2}$$•3\sqrt{2}$=18.
故答案为:18.
点评 本题考查截面面积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源: 题型:解答题
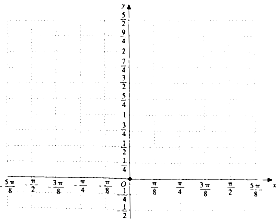 已知$\overrightarrow a=(sinx,cosx),\overrightarrow b=(sinx,sinx),f(x)=2\overrightarrow a•\overrightarrow b$.
已知$\overrightarrow a=(sinx,cosx),\overrightarrow b=(sinx,sinx),f(x)=2\overrightarrow a•\overrightarrow b$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,3] | B. | (0,2] | C. | [0,2) | D. | (0,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 四棱锥P-ABCD的三视图如图所示,其五个顶点都在同一球面上,若四棱锥P-ABCD的侧面积等于4(1+$\sqrt{2}$),则该外接球的表面积是( )
四棱锥P-ABCD的三视图如图所示,其五个顶点都在同一球面上,若四棱锥P-ABCD的侧面积等于4(1+$\sqrt{2}$),则该外接球的表面积是( )| A. | 4π | B. | 12π | C. | 24π | D. | 36π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
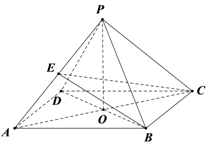 在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=$\sqrt{6}$,AC∩BD=O
在四棱锥P-ABCD中,底面是边长为2的菱形,∠BAD=60°,PB=PD=2,PA=$\sqrt{6}$,AC∩BD=O查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1009 | B. | -1008 | C. | -1007 | D. | -1006 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com