
分析 (Ⅰ)求出函数的导数,通过讨论m的范围,根据函数有且只有一个极值,求出m的范围即可;
(Ⅱ)不妨设-1<x1<1<x2,令g(x)=f(2-x)-f(x)(-1<x<1),根据函数的单调性证明即可.
解答 解:(Ⅰ)f(x)定义域为(-1,+∞),
$f'(x)=\frac{2}{x+1}+mx-({m+1})=\frac{{m{x^2}-x+1-m}}{x+1}=\frac{(x-1)(mx+m-1)}{x+1}$…(2分)
即求f'(x)=0在区间(-1,+∞)上只有一个解,
(1)当m≠0时,由f'(x)=0得x=1或$x=\frac{1}{m}-1$,
则$\frac{1}{m}-1<-1$,m<0…(4分)
(2)当m=0时,$f'(x)═\frac{-x+1}{x+1}=0$.得x=1符合题意,
综上:当m≤0时,f(x)有且只有一个极值 …(6分)
(Ⅱ)由(Ⅰ)知:m≤0,x=1时f(x)有且只有一个极大值.
又f(x1)=f(x2)(x1≠x2),不妨设-1<x1<1<x2
令g(x)=f(2-x)-f(x)(-1<x<1)
则g(x)=2ln(3-x)-2ln(x+1)+2x-2(m+1)$g'(x)=\frac{-2}{3-x}-\frac{2}{x+1}+2=\frac{{-2{{({x-1})}^2}}}{{({x+1})({3-x})}}≤0$
所以g(x)在(-1,1)上为减函数,故g(x)>g(1)=0…(10分)
即当-1<x<1时,f(2-x)>f(x).
所以f(2-x1)>f(x1)=f(x2),即f(2-x1)>f(x2)
由(Ⅰ)知,f(x)在(1,+∞)上为减函数,且2-x1>1,x2>1,
所以2-x1<x2,故x1+x2>2.…(12分)
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及不等式的证明,是一道综合题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
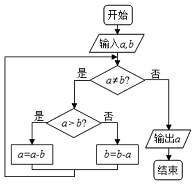 下面程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为8,12,则输出的a=( )
下面程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为8,12,则输出的a=( )| A. | 2 | B. | 0 | C. | 4 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $8\sqrt{2}π$ | B. | $8(3-\sqrt{2})π$ | C. | $16(\sqrt{2}-1)π$ | D. | $16(2-\sqrt{2})π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0<x1x2<1 | B. | x1x2=1 | C. | 1<x1x2<e | D. | x1x2>e |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
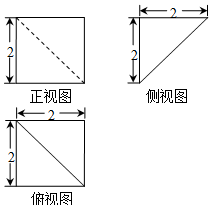
| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8\sqrt{2}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com