练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．（Ⅰ）计算：${（{\sqrt{2}-1}）^0}-\sqrt{\frac{1}{{4×{3^2}}}}+\frac{1}{{{2^2}×\sqrt{2+{2^{-2}}}}}$；
    （Ⅱ）若tanx=2，求值：$\frac{2sin（π-x）-cosx}{{cosx-cos（\frac{3π}{2}-x）}}$．

    分析 （Ⅰ）由条件利用分数指数幂的运算法则求得要求式子的值．
    （Ⅱ）由条件利用同角三角函数的基本关系，求得要求式子的值．

    解答 （Ⅰ）解：${（{\sqrt{2}-1}）^0}-\sqrt{\frac{1}{{4×{3^2}}}}+\frac{1}{{{2^2}×\sqrt{2+{2^{-2}}}}}$=1-$\frac{1}{6}$+$\frac{1}{4•\frac{3}{2}}$=1．
    （Ⅱ）解：∵tanx=2，∴$\frac{2sin（π-x）-cosx}{{cosx-cos（\frac{3π}{2}-x）}}$=$\frac{2sinx-cosx}{cosx+sinx}=\frac{2tanx-1}{1+tanx}=\frac{2×2-1}{1+2}=1$．

    点评 本题主要考查分数指数幂的运算法则，同角三角函数的基本关系，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    20．已知函数f（x）是定义在R上的偶函数，当x≥0时，f（x）=x（x-2）．
    （1）画出函数f（x）的图象；
    （2）写出函数的解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．$\frac{{\sqrt{3}-tan{{15}^0}}}{{\sqrt{3}tan{{15}^0}+1}}$=（　　）
    A．-1B．$\frac{{\sqrt{3}}}{3}$C．1D．$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知函数f（x）=ln|x-2|-|x-2|，则它的图象大致是（　　）
    A．B．
    C．D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

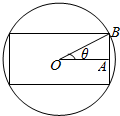    5．把截面半径为5的圆形木头锯成面积为y的矩形木料，如图，点O为圆心，OA⊥OB，设∠AOB=θ，把面积y表示为θ的表达式，则有（　　）
    A．y=50cos2θB．y=25sinθC．y=25sin2θD．y=50sin2θ

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．若cosθ=$\frac{3}{5}$（-$\frac{π}{2}$＜θ＜0），则cos（θ-$\frac{π}{6}$）的值是（　　）
    A．$\frac{3\sqrt{3}±4}{10}$B．$\frac{4±3\sqrt{3}}{10}$C．$\frac{3\sqrt{3}-4}{10}$D．$\frac{3\sqrt{3}+4}{10}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    2．若函数f（x）=3x2-5x+a的一个零点在区间（-2，0）内，另一个零点在区间（1，3）内，则实数a的取值范围是（-12，0）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．已知$\left\{\begin{array}{l}{x-y+1≥0}\\{x+y-1≥0}\\{y≥-1}\end{array}\right.$，求：
    （Ⅰ）z=x+2y-4的最大值；
    （Ⅱ）z=$\frac{2y+1}{x+1}$的范围；
    （III）z=x2+y2-10y+25的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．在△ABC中，若A=120°，AB=5，BC=7，则sinB=$\frac{3\sqrt{3}}{14}$．

    查看答案和解析>>

    同步练习册答案