
变量x、y满足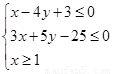
(1)设z=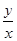 ,求z的最小值;
,求z的最小值;
(2)设z=x2+y2,求z的取值范围.
(1)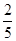 ;(2)
;(2)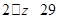 .
.
【解析】
试题分析: 由题意画出可行域,分别求出可行域各顶点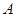 、
、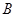 、
、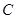 坐标.(1)将所求目标函数
坐标.(1)将所求目标函数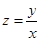 构造为
构造为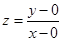 ,此时
,此时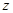 可以看作是可行域内的点与原点连成直线的斜率的最小值,由于可行域范围在第一象限内,所以可行域内的点与原点连线中倾斜角最小的为
可以看作是可行域内的点与原点连成直线的斜率的最小值,由于可行域范围在第一象限内,所以可行域内的点与原点连线中倾斜角最小的为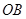 ,故
,故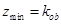 ,再由顶点
,再由顶点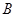 坐标可求出
坐标可求出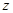 的最小值;(2)将目标函数
的最小值;(2)将目标函数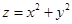 构造为
构造为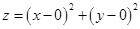 ,此时
,此时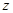 可以看作是可行域内的点与原点之间距离的范围,经查验比较可得
可以看作是可行域内的点与原点之间距离的范围,经查验比较可得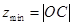 ,
,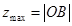 ,通过计算
,通过计算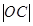 、
、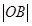 的值可以求出所求
的值可以求出所求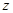 的取值范围.提示:在解决此类线性规划问题中,常常把目标函数构造出斜截式的直线方程
的取值范围.提示:在解决此类线性规划问题中,常常把目标函数构造出斜截式的直线方程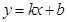 、过原点直线的斜率
、过原点直线的斜率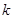 、与某一定点间的距离
、与某一定点间的距离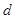 等等,再通过求截距、斜率、距离来求出目标函数的值.
等等,再通过求截距、斜率、距离来求出目标函数的值.
试题解析:由约束条件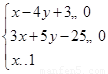 ,作出
,作出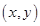 可行域如图所示.
可行域如图所示.
 3分
3分
由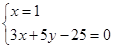 ,解得
,解得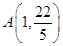
由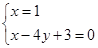 ,解得
,解得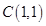
由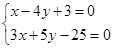 ,解得
,解得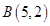 . 6分
. 6分
(1)因为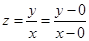 ,所以
,所以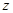 的值即是可行域中的点与原点
的值即是可行域中的点与原点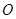 连线的斜率.
连线的斜率.
观察图形可知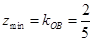 9分
9分
(2)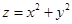 的几何意义是可行域上的点到原点
的几何意义是可行域上的点到原点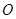 的距离的平方,
的距离的平方,
结合图形可知,可行域上的点到原点的距离中,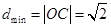 ,
,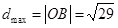 ,
,
所以所求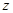 的取值范围为
的取值范围为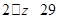 .
.
考点:1线性规划问题;2.斜率的计算.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:
两个相关变量x,y满足如下关系:
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com