
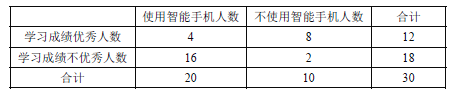
【题目】某研究型学习小组调查研究”中学生使用智能手机对学习的影响”.部分统计数据如下表:
参考数据:

参考公式: 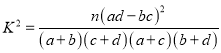 ,其中
,其中![]()
(Ⅰ)试根据以上数据,运用独立性检验思想,指出有多大把握认为中学生使用智能手机对学习有影响?
(Ⅱ)研究小组将该样本中使用智能手机且成绩优秀的4位同学记为![]() 组,不使用智能手机且成绩优秀的8位同学记为
组,不使用智能手机且成绩优秀的8位同学记为![]() 组,计划从
组,计划从![]() 组推选的2人和
组推选的2人和![]() 组推选的3人中,随机挑选两人在学校升旗仪式上作“国旗下讲话”分享学习经验.求挑选的两人恰好分别来自
组推选的3人中,随机挑选两人在学校升旗仪式上作“国旗下讲话”分享学习经验.求挑选的两人恰好分别来自![]() 、
、![]() 两组的概率.
两组的概率.
【答案】(1)该研究小组有99.5%的把握认为中学生使用智能手机对学习有影响;(2) ![]() .
.
【解析】试题分析:(Ⅰ)根据![]() 列联表,计算
列联表,计算![]() ,对比参考数据,
,对比参考数据, ![]() 且
且![]() ,所以有99.5%的把握认为中学生使用智能手机对学习有影响;(Ⅱ)将
,所以有99.5%的把握认为中学生使用智能手机对学习有影响;(Ⅱ)将![]() 组中的2人,和
组中的2人,和![]() 组中的3人编号,列举所有挑选两人的基本事件的个数,和其中分别来自
组中的3人编号,列举所有挑选两人的基本事件的个数,和其中分别来自![]() 两组的基本事件的个数,最后相除就是所求概率.
两组的基本事件的个数,最后相除就是所求概率.
试题解析:(Ⅰ)根据上方公式求得![]() ,
,
因为![]()
所以该研究小组有99.5%的把握认为中学生使用智能手机对学习有影响.
(Ⅱ)记![]() 组推选的两名同学为
组推选的两名同学为![]() ,
, ![]() 组推选的三名同学为
组推选的三名同学为![]() ,
,
则从中随机选出两名同学包含如下10个基本事件:
![]()
记挑选的两人恰好分别来自![]() 两组为事件
两组为事件![]() ,
,
则事件![]() 包含如下6 个基本事件:
包含如下6 个基本事件:
![]()
故![]() .
.
即挑选的两人恰好分别来自![]() 两组的概率是
两组的概率是![]() .
.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
【题目】交强险是车主必须为机动车购买的险种,若普通![]() 座以下私家车投保交强险第一年的费用(基准保费)统一为
座以下私家车投保交强险第一年的费用(基准保费)统一为![]() 元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:
元,在下一年续保时,实行的是费率浮动机制,保费与上一年度车辆发生道路交通事故的情况相联系,发生交通事故的次数越多,费率也就越高,具体浮动情况如下表:

某机构为了研究某一品牌普通![]() 座以下私家车的投保情况,随机抽取了
座以下私家车的投保情况,随机抽取了![]() 辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
辆车龄已满三年的该品牌同型号私家车的下一年续保时的情况,统计得到了下面的表格:
类型 |
|
|
|
|
|
|
数量 | 10 | 5 | 5 | 20 | 15 | 5 |
以这![]() 辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
辆该品牌车的投保类型的频率代替一辆车投保类型的概率,完成下列问题:
(Ⅰ)按照我国《机动车交通事故责任强制保险条例》汽车交强险价格的规定, ![]() ,记
,记![]() 为某同学家里的一辆该品牌车在第四年续保时的费用,求
为某同学家里的一辆该品牌车在第四年续保时的费用,求![]() 的分布列与数学期望;(数学期望值保留到个位数字)
的分布列与数学期望;(数学期望值保留到个位数字)
(Ⅱ)某二手车销售商专门销售这一品牌的二手车,且将下一年的交强险保费高于基本保费的车辆记为事故车,假设购进一辆事故车亏损![]() 元,一辆非事故车盈利
元,一辆非事故车盈利![]() 元:
元:
①若该销售商购进三辆(车龄已满三年)该品牌二手车,求这三辆车中至少有一辆事故车的概率;
②若该销售商一次购进![]() 辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
辆(车龄已满三年)该品牌二手车,求他获得利润的期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一种饮料每箱装有6听,经检测,某箱中每听的容量(单位:ml)如以下茎叶图所示.
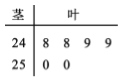
(Ⅰ)求这箱饮料的平均容量和容量的中位数;
(Ⅱ)如果从这箱饮料中随机取出2听饮用,求取到的2听饮料中至少有1听的容量为250ml的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
(Ⅰ)讨论函数![]() 的单调区间与极值;
的单调区间与极值;
(Ⅱ)若![]() 且
且![]() 恒成立,求
恒成立,求![]() 的最大值;
的最大值;
(Ⅲ)在(Ⅱ)的条件下,且![]() 取得最大值时,设
取得最大值时,设![]() ,且函数
,且函数![]() 有两个零点
有两个零点![]() ,求实数
,求实数![]() 的取值范围,并证明:
的取值范围,并证明: ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com