【题目】某同学为研究“网络游戏对当代青少年的影响”作了一次调查，共调查了50名同学，其中男生26人，有8人不喜欢玩游戏，而调查的女生中有9人喜欢玩游戏.
（1）根据以上数据完成2×2的列联表；
（2）根据以上数据，在犯错误的概率不超过0.025的前提下，能否认为“喜欢玩电脑游戏与性别有关系”？
男生 | 女生 | 总计 | |
喜欢玩游戏 | |||
不喜欢玩游戏 | |||
总计 |
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
科目：高中数学 来源： 题型：
【题目】下列事件：①任取这三条线段，这三条线段恰好组成直角三角形；②从一个三角形的三个顶点各任画一条射线，这三条射线交于一点；③实数
，
都不为，但
；④明年12月28日的最高气温高于今年12月28日的最高气温.其中为随机事件的是（ ）
A.①②③④B.①②④C.①③④D.②③④
查看答案和解析>>
科目：高中数学 来源： 题型：
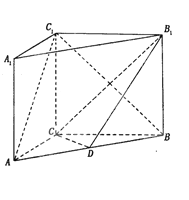
【题目】如图所示, 在直三棱柱ABC－A1B1C1中，AC＝3，BC＝4，AB=5，AA1＝4，点D是AB的中点，
（1）求证： AC1//平面CDB1；
（2）求二面角C1-AB-C的平面角的正切值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】根据调查，某学校开设了“街舞”、“围棋”、“武术”三个社团，三个社团参加的人数如下表所示：
社团 | 街舞 | 围棋 | 武术 |
人数 | 320 | 240 | 200 |
为调查社团开展情况，学校社团管理部采用分层抽样的方法从中抽取一个容量为n的样本，已知从“围棋”社团抽取的同学比从“街舞”社团抽取的同学少2人.
（1）求三个社团分别抽取了多少同学；
（2）若从“围棋”社团抽取的同学中选出2人担任该社团活动监督的职务，已知“围棋”社团被抽取的同学中有2名女生，求至少有1名女同学被选为监督职务的概率。
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某学校有n个班（n为给定正整数），且每班的男生与女生人数至多相差1．现该学校进行乒乓球比赛，规则如下：同一班的选手之间不比赛，不同班的每两名选手都比赛一场．我们称在同性别选手间的比赛为同打，异性别选手间的比赛为异打．若同打场数与异打场数至多相差1，求有奇数名学生的班级至多有多少个？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】心理学家分析发现视觉和空间能力与性别有关，某数学兴趣小组为了验证这个结论，从兴趣小组中按分层抽样的方法抽取
名同学（男
女
），给所有同学几何题和代数题各一题，让各位同学自由选择一道题进行解答.选题情况如下表：（单位：人）
几何题 | 代数题 | 总计 | |
男同学 |
|
|
|
女同学 |
|
|
|
总计 |
|
|
|
（1）能否据此判断有
的把握认为视觉和空间能力与性别有关？
（2）经过多次测试后，甲每次解答一道几何题所用的时间在
分钟，乙每次解答一道几何题所用的时间在
分钟，现甲、乙各解同一道几何题，求乙比甲先解答完的概率.
（3）现从选择做几何的
名女生中任意抽取两人对她们的答题情况进行全程研究，记甲、乙两女生被抽到的人数为
，求的分布列及数学期望
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设椭圆
的方程为
，点
为坐标原点，点
，
的坐标分别为
，
，
，直线
的斜率为
.
（1）求椭圆的方程；
（2）若斜率为
的直线
交椭圆于
，
两点，交
轴于点
，问是否存在实数
使得以
为直径的圆恒过点？若存在，求的值；若不存在，说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知正方体ABCD－A1B1C1D1的棱长为1，E，F分别是棱AD，B1C1上的动点，设AE＝λ，B1F＝μ．若平面BEF与正方体的截面是五边形，则λ＋μ的取值范围是________．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
