练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    13．学校组织“踢毽球”大赛，某班为了选出一人参加比赛，对班上甲乙两位同学进行了8次测试，且每次测试之间是相互独立．成绩如下：（单位：个/分钟）
    甲8081937288758384
    乙8293708477877885
    （1）用茎叶图表示这两组数据；
    （2）从统计学的角度考虑，你认为选派那位学生参加比赛合适，请说明理由？
    （3）若将频率视为概率，对甲同学在今后的三次比赛成绩进行预测，记这三次成绩高于79个/分钟的次数为ξ，求ξ的分布列及数学期望Eξ．
    （参考数据：22+12+112+102+62+72+12+22=316，02+112+122+22+52+52+42+32）

    分析 （1）以十位数为茎，个位数为叶，由已知条件能作出甲乙两同学“踢毽球”的茎叶图．
    （2）求出$\overline{{x}_{甲}}$，$\overline{{x}_{乙}}$，${{S}_{甲}}^{2}$，${{S}_{乙}}^{2}$，由于甲、乙的平均成绩相等，而甲的方差较小，得到派甲参赛比较合适．
    （3）由题意可知，ξ的取值为0，1，2，3，分别求出相应的概率，由此能求出ξ的分布列及数学期望Eξ．

    解答 解：（1）以十位数为茎，个位数为叶，由已知作出甲乙两同学“踢毽球”的茎叶图如下图：

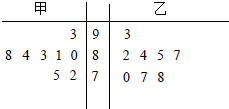
    （2）$\overline{{x}_{甲}}$=$\frac{80+81+93+72+88+75+83+84}{8}$=82，
    $\overline{{x}_{乙}}$=$\frac{82+93+70+84+77+87+78+85}{8}$=82，
    ${{S}_{甲}}^{2}$=$\frac{{2}^{2}+{1}^{2}+1{1}^{2}+1{0}^{2}+{6}^{2}+{7}^{2}+{1}^{2}+{2}^{2}}{8}$=39.5，
    ${{S}_{乙}}^{2}$=$\frac{{0}^{2}+1{2}^{2}+1{2}^{2}+{2}^{2}+{5}^{2}+{5}^{2}+{4}^{2}+{3}^{2}}{8}$=43，
    由于甲、乙的平均成绩相等，而甲的方差较小，所以甲的成绩较稳定，派甲参赛比较合适．
    （3）由题意可知，ξ的取值为0，1，2，3，
    由表格可知：高于79个/分钟的频率为$\frac{3}{4}$，则高于79个/分钟的概率为$\frac{3}{4}$，
    则P（ξ=0）=（1-$\frac{3}{4}$）3=$\frac{1}{64}$，
    P（ξ=1）=${C}_{3}^{1}×\frac{3}{4}×（1-\frac{3}{4}）$2=$\frac{9}{64}$，
    P（ξ=2）=${C}_{3}^{2}（\frac{3}{4}）^{2}×（1-\frac{3}{4}）$=$\frac{27}{64}$，
    P（ξ=3）=$（\frac{3}{4}）^{3}$=$\frac{27}{64}$，
    ∴ξ的分布列如下：

    ξ0123
    P$\frac{1}{64}$$\frac{9}{64}$$\frac{27}{64}$$\frac{27}{64}$
    ∴Eξ=$0×\frac{1}{64}+1×\frac{9}{64}+2×\frac{27}{64}+3×\frac{27}{64}$=$\frac{9}{4}$．

    点评 本题考查了茎叶图，方差，离散型随机变量的分布列和数学期望的求法，是中档题，解题时要认真审题，注意排列组合知识的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    3．已知tan（-α-$\frac{4}{3}$π）=-5，则tan（$\frac{π}{3}$+α）的值为（　　）
    A．5B．-5C．±5D．不确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．数列{an}中，a1=1，an+1=$\frac{{a}_{n}}{2{a}_{n}+1}$，试推测出数列{an}的通项公式为an=$\frac{1}{2n-1}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．设α，β是两个不同的平面，l，m是两条不同的直线，命题p：α∥β，l?α，m?β，则l∥m；命题q：l∥α，m⊥l，m?β，则β⊥α．下列命题为真命题的是（　　）
    A．p或qB．p且qC．p或qD．p且q

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．已知关于x的函数f（x）=m（x2-4x+lnx）-（2m2+1）x+2lnx，其中m∈R，其在点B（1，0）处的切线所对应的函数为g（x）=0．
    （1）已知函数f（x）的图象与直线y=k2-2k无公共点，求实数k的取值范围；
    （2）已知p≤0，若对任意的x∈[1，2]，总有f（x）≥$\frac{（p-2）x}{2}$+$\frac{p+2}{2x}$+2x-x2成立，求实数p的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知x，y满足约束条件$\left\{{\begin{array}{l}{0≤x≤2}\\{x+y-2≥0}\\{kx-y+2≥0（k＞0）}\end{array}}\right.$，若目标函数z=x+2y的最大值为10，则k的值为（　　）
    A．$\frac{1}{2}$B．$\frac{1}{3}$C．1D．2

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．设二次函数f（x）满足：f（0）=-1，f（x）-2=0的两根分别为-3和1．
    （1）求f（x）的解析式．
    （2）在区间[0，2]上，y=f（x）的图象恒在直线y=kx-3的上方，求k的范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知f（x）=$\sqrt{3}$sinx-cosx，f′（x）是f（x）的导函数，若f（x0）=$\frac{1}{2}$，则f′（2x0-$\frac{π}{6}$）=（　　）
    A．-$\frac{7}{8}$B．$\frac{7}{8}$C．-$\frac{7}{4}$D．$\frac{7}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．已知向量$\overrightarrow{a}$=（1，2），$\overrightarrow{b}$=（m，4），且 $\overrightarrow{a}$∥（2$\overrightarrow{a}$+$\overrightarrow{b}$），则实数m的值为2．

    查看答案和解析>>

    同步练习册答案