
【题目】已知椭圆C: ![]() =1过点A(2,0),B(0,1)两点.
=1过点A(2,0),B(0,1)两点.
(1)求椭圆C的方程及离心率;
(2)设P为第三象限内一点且在椭圆C上,直线PA与y轴交于点M,直线PB与x轴交于点N,求证:四边形ABNM的面积为定值.
【答案】
(1)
解:∵椭圆C: ![]() =1过点A(2,0),B(0,1)两点,
=1过点A(2,0),B(0,1)两点,
∴a=2,b=1,则 ![]() =
= ![]() ,
,
∴椭圆C的方程为 ![]() ,离心率为e=
,离心率为e= ![]()
(2)
证明:如图, 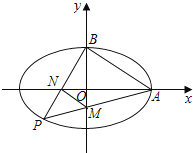
设P(x0,y0),则 ![]() ,PA所在直线方程为
,PA所在直线方程为 ![]() ,
,
取x=0,得 ![]() ;
;
![]() ,PB所在直线方程为
,PB所在直线方程为 ![]() ,
,
取y=0,得 ![]() .
.
∴|AN|= ![]() ,
,
|BM|=1﹣ ![]() .
.
∴ ![]() =
= ![]() =
= ![]() =
= ![]()
= ![]()
![]() =
= ![]() .
.
∴四边形ABNM的面积为定值2.
【解析】(1)由题意可得a=2,b=1,则 ![]() ,则椭圆C的方程可求,离心率为e=
,则椭圆C的方程可求,离心率为e= ![]() ;(2)设P(x0 , y0),求出PA、PB所在直线方程,得到M,N的坐标,求得|AN|,|BM|.由
;(2)设P(x0 , y0),求出PA、PB所在直线方程,得到M,N的坐标,求得|AN|,|BM|.由 ![]() ,结合P在椭圆上求得四边形ABNM的面积为定值2.;本题考查椭圆的标准方程,考查了椭圆的简单性质,考查计算能力与推理论证能力,是中档题.
,结合P在椭圆上求得四边形ABNM的面积为定值2.;本题考查椭圆的标准方程,考查了椭圆的简单性质,考查计算能力与推理论证能力,是中档题.
【考点精析】通过灵活运用椭圆的标准方程,掌握椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 即可以解答此题.
即可以解答此题.


科目:高中数学 来源: 题型:
【题目】已知函数f(x)=kax-a-x(a>0且a≠1)是R上的奇函数.
(Ⅰ)求常数k的值;
(Ⅱ)若a>1,试判断函数f(x)的单调性,并加以证明;
(Ⅲ)若a=2,且函数g(x)=a2x+a-2x-2mf(x)在[0,1]上的最小值为1,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】由![]() ,
,![]() ,
,![]() ,
,![]() 排列而成的
排列而成的![]() 项数列
项数列![]() 满足:每项都大于它之前的所有项或者小于它之前的所有项.
满足:每项都大于它之前的所有项或者小于它之前的所有项.
(![]() )满足条件的数列中,写出所有的单调数列.
)满足条件的数列中,写出所有的单调数列.
(![]() )当
)当![]() 时,写出所有满足条件的数列.
时,写出所有满足条件的数列.
(![]() )满足条件的数列
)满足条件的数列![]() 的个数是多少?并证明你的结论.
的个数是多少?并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4x+3sinx,x∈(-1,1),如果f(1-a)+f(1-a2)<0成立,则实数a的取值范围为( )
A. (0,1) B. ![]() C.
C. ![]() D. (-∞,-2)∪(1,+∞)
D. (-∞,-2)∪(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(ax+1)(x≥0,a>0), ![]() .
.
(1)讨论函数y=f(x)-g(x)的单调性;
(2)若不等式f(x)≥g(x)+1在x∈[0,+∞)时恒成立,求实数a的取值范围;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于每项均是正整数的数列A:a1,a2,…,an,定义变换T1,T1将数列A变换成数列T1(A):n,a1-1,a2-1,…,an-1.对于每项均是非负整数的数列B:b1,b2,…,bm,定义变换T2,T2将数列B各项从大到小排列,然后去掉所有为零的项,得到数列T2(B).又定义S(B)=2(b1+2b2+…+mbm)+![]() +
+![]() +…+
+…+![]() .设A0是每项均为正整数的有穷数列,令Ak+1=T2(T1(Ak))(k=0,1,2,…).
.设A0是每项均为正整数的有穷数列,令Ak+1=T2(T1(Ak))(k=0,1,2,…).
(1)如果数列A0为2,6,4,8,写出数列A1,A2;
(2)对于每项均是正整数的有穷数列A,证明:S(T1(A))=S(A);
(3)证明:对于任意给定的每项均为正整数的有穷数列A0,存在正整数K,当k≥K时,S(Ak+1)=S(Ak).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com