练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    用反证法证明命题“a，b∈N，如果ab可被5整除，那么a，b至少有1个能被5整除．”则假设的内容是（ ）

    A.a，b都能被5整除 B.a，b都不能被5整除

    C.a，b不能被5整除 D.a，b有1个不能被5整除

     

    B

    【解析】

    试题分析：反设是一种对立性假设，即想证明一个命题成立时，可以证明其否定不成立，由此得出此命题是成立的．

    【解析】
    由于反证法是命题的否定的一个运用，故用反证法证明命题时，可以设其否定成立进行推证．

    命题“a，b∈N，如果ab可被5整除，那么a，b至少有1个能被5整除．”的否定是“a，b都不能被5整除”．

    故应选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 4.2数学归纳法证明不等式举例（解析版） 题型：选择题

    用数学归纳法证明不等式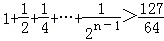成立，起始值至少应取为（ ）

    A.7 B.8 C.9 D.10

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 3.1二维形式柯西不等式练习卷（解析版） 题型：填空题

    （2014•陕西三模）已知a、b、c、d均为正数，且a2+b2=4，cd=1，则（a2c2+b2d2）（b2c2+a2d2）的最小值为 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 3.1二维形式柯西不等式练习卷（解析版） 题型：选择题

    （2014•孝感二模）已知x，y，z均为正数，且x+y+z=2，则++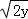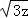的最大值是（ ）

    A.2 B.2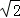 C.2 D.?3

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 2.3反证法与放缩法练习卷（解析版） 题型：选择题

    用反证法证明：“方程ax2+bx+c=0，且a，b，c都是奇数，则方程没有整数根”正确的假设是方程存在实数根x0为（ ）

    A.整数 B.奇数或偶数 C.正整数或负整数 D.自然数或负整数

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 2.3反证法与放缩法练习卷（解析版） 题型：选择题

    用反证法证明命题“若a2+b2=0，则a、b全为0（a、b∈R）”，其反设正确的是（ ）

    A.a、b至少有一个不为0 B.a、b至少有一个为0

    C.a、b全不为0 D.a、b中只有一个为0

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 2.2综合法与分析法练习卷（解析版） 题型：填空题

    下列表述：

    ①综合法是执因导果法；

    ②综合法是顺推法；

    ③分析法是执果索因法；

    ④分析法是间接证法；

    ⑤反证法是逆推法．

    正确的语句有是 （填序号）．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 2.1比较法练习卷（解析版） 题型：填空题

    下列不等式的证明明过程：

    ①若a，b∈R，则 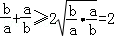②若x，y∈R，则；

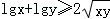    ③若x∈R，则；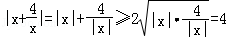

    ④若a，b∈R，ab＜0，则．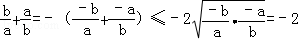

    其中正确的序号是 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 1.2绝对值不等式练习卷（解析版） 题型：选择题

    （2014•衡阳三模）设函数f（x）=|x2﹣2x﹣1|，若a＞b＞1，且f（a）=f（b），则ab﹣a﹣b的取值范围为（ ）

    A.（﹣2，3） B.（﹣2，2） C.（1，2） D.（﹣1，1）

     

    查看答案和解析>>

    同步练习册答案