练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    用反证法证明：“方程ax2+bx+c=0，且a，b，c都是奇数，则方程没有整数根”正确的假设是方程存在实数根x0为（ ）

    A.整数 B.奇数或偶数 C.正整数或负整数 D.自然数或负整数

     

    A

    【解析】

    试题分析：本题考查反证法的概念，逻辑用语，否命题与命题的否定的概念，逻辑词语的否定．根据反证法的步骤，假设是对原命题结论的否定，故只须对“方程没有整数根”写出否定即可．

    【解析】
    根据反证法的步骤，假设是对原命题结论的否定

    “方程没有整数根”的否定“方程存在实数根x0为整数”．

    即假设正确的是：方程存在实数根x0为整数．

    故选A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 4.2数学归纳法证明不等式举例（解析版） 题型：填空题

    设，则f（k+1）﹣f（k）= ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 3.2一般形式柯西不等式练习卷（解析版） 题型：选择题

    （2012•湖北）设a，b，c，x，y，z是正数，且a2+b2+c2=10，x2+y2+z2=40，ax+by+cz=20，则=（ ）

    A.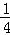 B. C. D.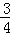

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 3.1二维形式柯西不等式练习卷（解析版） 题型：选择题

    已知x2+4y2+kz2=36，且x+y+z的最大值为7，则正数k等于（ ）

    A.1 B.4 C.8 D.9

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 2.3反证法与放缩法练习卷（解析版） 题型：选择题

    用反证法证明：“a＞b”，应假设为（ ）

    A.a＞b B.a＜b C.a=b D.a≤b

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 2.3反证法与放缩法练习卷（解析版） 题型：选择题

    用反证法证明命题“a，b∈N，如果ab可被5整除，那么a，b至少有1个能被5整除．”则假设的内容是（ ）

    A.a，b都能被5整除 B.a，b都不能被5整除

    C.a，b不能被5整除 D.a，b有1个不能被5整除

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 2.3反证法与放缩法练习卷（解析版） 题型：选择题

    用反证法证明命题：“已知a，b为实数，则方程x2+ax+b=0至少有一个实根”时，要做的假设是（ ）

    A.方程x2+ax+b=0没有实根

    B.方程x2+ax+b=0至多有一个实根

    C.方程x2+ax+b=0至多有两个实根

    D.方程x2+ax+b=0恰好有两个实根

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 2.2综合法与分析法练习卷（解析版） 题型：选择题

    关于综合法和分析法说法错误的是（ ）

    A.综合法和分析法是直接证明中最基本的两种证明方法

    B.综合法又叫顺推证法或由因导果法

    C.分析法又叫逆推证法或执果索因法

    D.综合法和分析法都是因果分别互推的两头凑法

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 1.2绝对值不等式练习卷（解析版） 题型：选择题

    （2014•江西二模）若存在x∈R，使|2x﹣a|+2|3﹣x|≤1成立，则实数a的取值范围是（ ）

    A.[2，4] B.（5，7） C.[5，7] D.（﹣∞，5]∪[7，+∞）

     

    查看答案和解析>>

    同步练习册答案