练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知x2+4y2+kz2=36，且x+y+z的最大值为7，则正数k等于（ ）

    A.1 B.4 C.8 D.9

     

    D

    【解析】

    试题分析：由柯西不等式可得 （x2+4y2+kz2）（1++）≥（x+y+z）2，再根据x+y+z的最大值为7，可得36（1++）=49，由此求得正数k的值．

    【解析】
    由题意利用柯西不等式可得 （x2+4y2+kz2）（1++）≥（x+y+z）2，

    即 36（1++）≥（x+y+z）2．

    再根据x+y+z的最大值为7，可得36（1++）=49，求得正数k=9，

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：[同步]2014年新人教A版选修4-6 1.1整除练习卷（解析版） 题型：选择题

    下列各数中最小的数是（ ）

    A.85（9） B.210（6） C.1000（4） D.11111（2）

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 3.3排序不等式练习卷（解析版） 题型：解答题

    设a，b，c为正数，利用排序不等式证明a3+b3+c3≥3abc．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 3.1二维形式柯西不等式练习卷（解析版） 题型：填空题

    （2014•陕西三模）已知a、b、c、d均为正数，且a2+b2=4，cd=1，则（a2c2+b2d2）（b2c2+a2d2）的最小值为 ．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 3.1二维形式柯西不等式练习卷（解析版） 题型：选择题

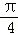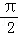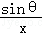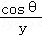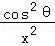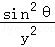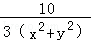    已知x，y均为正数，θ∈（，），且满足=，+=，则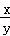的值为（ ）

    A.2 B.1 C.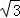 D.

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 3.1二维形式柯西不等式练习卷（解析版） 题型：选择题

    （2014•孝感二模）已知x，y，z均为正数，且x+y+z=2，则++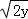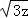的最大值是（ ）

    A.2 B.2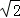 C.2 D.?3

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 2.3反证法与放缩法练习卷（解析版） 题型：选择题

    用反证法证明：“方程ax2+bx+c=0，且a，b，c都是奇数，则方程没有整数根”正确的假设是方程存在实数根x0为（ ）

    A.整数 B.奇数或偶数 C.正整数或负整数 D.自然数或负整数

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 2.2综合法与分析法练习卷（解析版） 题型：填空题

    下列表述：

    ①综合法是执因导果法；

    ②综合法是顺推法；

    ③分析法是执果索因法；

    ④分析法是间接证法；

    ⑤反证法是逆推法．

    正确的语句有是 （填序号）．

     

    查看答案和解析>>

    科目：高中数学 来源：[同步]2014年新人教A版选修4-5 1.2绝对值不等式练习卷（解析版） 题型：选择题

    （2013•红桥区二模）集合A={x||x﹣2|≤2}，B={y|y=﹣x2，﹣1≤x≤2}，则A∩B=（ ）

    A.{x|﹣4≤x≤4} B.{x|x≠0} C.{0} D.∅

     

    查看答案和解析>>

    同步练习册答案