
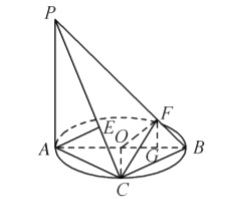
【题目】如图,![]() 垂直于
垂直于![]() 所在的平面
所在的平面![]() ,
,![]() 为
为![]() 的直径,
的直径,![]() 是弧
是弧![]() 上的一个动点(不与端点
上的一个动点(不与端点![]() 重合),
重合),![]() 为
为![]() 上一点,且
上一点,且![]() 是线段
是线段![]() 上的一个动点(不与端点
上的一个动点(不与端点![]() 重合).
重合).

(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 是弧
是弧![]() 的中点,
的中点,![]() 是锐角,且三棱锥
是锐角,且三棱锥![]() 的体积为
的体积为![]() ,求
,求![]() 的值.
的值.
【答案】(1)见证明;(2)![]()
【解析】
(1)由![]() 为
为![]() 的直径,得到
的直径,得到![]() ,又由
,又由![]() 平面
平面![]() ,证得
,证得![]() ,利用线面垂直的判定定理得到
,利用线面垂直的判定定理得到![]() 平面
平面![]() ,再利用线面垂直的判定定理,即可证得
,再利用线面垂直的判定定理,即可证得![]() 平面
平面![]() .
.
(2)当点![]() 位于线段
位于线段![]() 上时,如图所示:作
上时,如图所示:作![]() ,垂足为点
,垂足为点![]() ,根据线面垂直的判定定,证得
,根据线面垂直的判定定,证得![]() 平面
平面![]() ,得到
,得到![]() 是三棱锥
是三棱锥![]() 的底面
的底面![]() 上的高,再来体积公式,列出方程,即可求解.
上的高,再来体积公式,列出方程,即可求解.
(1)证明:因为![]() 为
为![]() 的直径,
的直径,
所以根据直径所对的圆周角是直角,可知![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为![]() 平面
平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(2)当点![]() 位于线段
位于线段![]() 上时,如图所示:作
上时,如图所示:作![]() ,垂足为点
,垂足为点![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
又因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() 是三棱锥
是三棱锥![]() 的底面
的底面![]() 上的高,
上的高,
因为![]() 是弧
是弧![]() 的中点,且
的中点,且![]() ,
,
所以![]() ,且
,且![]() ,
,
若三棱锥![]() 的体积为
的体积为![]() ,
,
则![]() ,解得
,解得![]() ,
,
所以![]() ,所以
,所以![]() ,
,
所以 ,
,
综上所述,当三棱锥![]() 的体积为
的体积为![]() 时,
时,![]() .
.


科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),圆
为参数),圆![]() 的方程为
的方程为![]() .以原点
.以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(Ⅰ)求直线![]() 及圆
及圆![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)若直线![]() 与圆
与圆![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】阿基米德是古希腊伟大的哲学家、数学家、物理学家,对几何学、力学等学科作出过卓越贡献.为调查中学生对这一伟大科学家的了解程度,某调查小组随机抽取了某市的100名高中生,请他们列举阿基米德的成就,把能列举阿基米德成就不少于3项的称为“比较了解”,少于三项的称为“不太了解”他们的调查结果如下:

(1)完成如下![]() 列联表,并判断是否有99%的把握认为,了解阿基米德与选择文理科有关?
列联表,并判断是否有99%的把握认为,了解阿基米德与选择文理科有关?
(2)在抽取的100名高中生中,按照文理科采用分层抽样的方法抽取10人的样本.
(ⅰ)求抽取的文科生和理科生的人数;
(ⅱ)从10人的样本中随机抽取3人,用![]() 表示这3人中文科生的人数,求
表示这3人中文科生的人数,求![]() 的分布列和数学期望.参考数据:
的分布列和数学期望.参考数据:

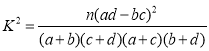 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位从一所学校招收某类特殊人才,对![]() 位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:
位已经选拔入围的学生进行运动协调能力和逻辑思维能力的测试,其测试结果如下表:

例如,表中运动协调能力良好且逻辑思维能力一般的学生有![]() 人.由于部分数据丢失,只知道从这
人.由于部分数据丢失,只知道从这![]() 位参加测试的学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生的概率为
位参加测试的学生中随机抽取一位,抽到运动协调能力或逻辑思维能力优秀的学生的概率为![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)从参加测试的![]() 位学生中任意抽取
位学生中任意抽取![]() 位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率;
位,求其中至少有一位运动协调能力或逻辑思维能力优秀的学生的概率;
(III)从参加测试的![]() 位学生中任意抽取
位学生中任意抽取![]() 位,设运动协调能力或逻辑思维能力优秀的学生人数为
位,设运动协调能力或逻辑思维能力优秀的学生人数为![]() ,求随机变量
,求随机变量![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() 也为抛物线
也为抛物线![]() 的焦点,点
的焦点,点![]() 为
为![]() 在第一象限的交点,且
在第一象限的交点,且![]() .
.
(I)求椭圆![]() 的方程;
的方程;
(II)延长![]() ,交椭圆
,交椭圆![]() 于点
于点![]() ,交抛物线
,交抛物线![]() 于点
于点![]() ,求三角形
,求三角形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,随着我国汽车消费水平的提高,二手车流通行业得到迅猛发展.某汽车交易市场对2017年成交的二手车交易前的使用时间(以下简称“使用时间”)进行统计,得到频率分布直方图如图1.
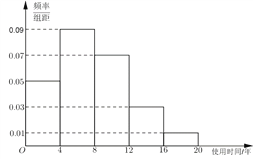

图1 图2
(1)记“在![]() 年成交的二手车中随机选取一辆,该车的使用年限在
年成交的二手车中随机选取一辆,该车的使用年限在![]() ”为事件
”为事件![]() ,试估计
,试估计![]() 的概率;
的概率;
(2)根据该汽车交易市场的历史资料,得到散点图如图2,其中![]() (单位:年)表示二手车的使用时间,
(单位:年)表示二手车的使用时间,![]() (单位:万元)表示相应的二手车的平均交易价格.由散点图看出,可采用
(单位:万元)表示相应的二手车的平均交易价格.由散点图看出,可采用![]() 作为二手车平均交易价格
作为二手车平均交易价格![]() 关于其使用年限
关于其使用年限![]() 的回归方程,相关数据如下表(表中
的回归方程,相关数据如下表(表中![]() ,
,![]() ):
):
|
|
|
|
|
|
5.5 | 8.7 | 1.9 | 301.4 | 79.75 | 385 |
①根据回归方程类型及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
②该汽车交易市场对使用8年以内(含8年)的二手车收取成交价格![]() 的佣金,对使用时间8年以上(不含8年)的二手车收取成交价格
的佣金,对使用时间8年以上(不含8年)的二手车收取成交价格![]() 的佣金.在图1对使用时间的分组中,以各组的区间中点值代表该组的各个值.若以2017年的数据作为决策依据,计算该汽车交易市场对成交的每辆车收取的平均佣金.
的佣金.在图1对使用时间的分组中,以各组的区间中点值代表该组的各个值.若以2017年的数据作为决策依据,计算该汽车交易市场对成交的每辆车收取的平均佣金.
附注:①对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为 ;
;
②参考数据:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100个网箱,测量各箱水产品的产量(单位:kg), 其频率分布直方图如下:

(1)记A表示事件“旧养殖法的箱产量低于50 kg”,估计A的概率;
(2)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:
箱产量<50 kg | 箱产量≥50 kg | |
旧养殖法 | ||
新养殖法 |
(3)根据箱产量的频率分布直方图,对这两种养殖方法的优劣进行比较.
附:
P( | 0.050 0.010 0.001 |
k | 3.841 6.635 10.828 |
![]() .
. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学专著《九章算术》中有一个“两鼠穿墙题”,其内容为:“今有垣厚五尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半.问何日相逢?各穿几何?”如图的程序框图源于这个题目,执行该程序框图,若输入x=20,则输出的结果为( )
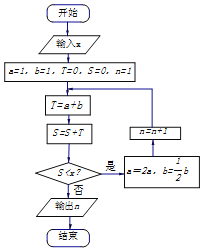
A. 3B. 4C. 5D. 6
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记![]() 为数列
为数列![]() 的前
的前![]() 项和.“任意正整数
项和.“任意正整数![]() ,均有
,均有![]() ”是“
”是“![]() 为递增数列”的
为递增数列”的
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com