练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知变量x、y满足条件，则2x+y的最大值是（　　）

    　

    A．

    3

    B．

    6

    C．

    9

    D．

    12


    C    

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知函数f（x）=2cos2x+2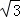sinxcosx+1．

    （Ⅰ）求函数f（x）的单调递增区间，最小正周期；

    （Ⅱ）画出f（x）的图象．（要求：列表，要有超过一个周期的图象，并标注关键点）

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知一元二次方程x2+2ax+（7a﹣6）=0（a∈R）有两个不等的实数根．

    （Ⅰ）求a的取值范围；

    （Ⅱ）求函数f（a）=a+的值域．

    　

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某同学在研究性学习中，收集到某制药厂车间工人数（单位：十人）与药品产量（单位：万盒）的数据如表所示：

    工人数：x（单位：十人）

    1

    2

    3

    4

    药品产量：y（单位：万盒）

    3

    4

    5

    6

    （1）请画出如表数据的散点图；

    （2）参考公式，根据表格提供的数据，用最小二乘法求出y关于x的线性回归方程y=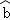x+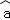；（参考数据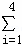i2=30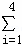，xiyi=50）

    （3）试根据（2）求出的线性回归方程，预测该制药厂车间工人数为45时，药品产量是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    不等式x2+3x﹣4＜0的解集为（　　）

    　

    A．

    {x|x＜﹣1，或x＞4}

    B．

    {x|﹣3＜x＜0}

    C．

    {x|x＜﹣4，或x＞1}

    D．

    {x|﹣4＜x＜1}

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设等差数列{an}的前n项和Sn，若S15＞0，S16＜0，则数列{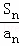}的前15项中最大的项是（　　）

    　

    A．

    第1项

    B．

    第8项

    C．

    第9项

    D．

    第15项

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知等差数列{an}，公差d≠0，a1=2，且a1，a3，a9成等比数列．

    （Ⅰ）求数列{an}的通项公式；

    （Ⅱ）求数列{2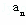﹣1}的前n项和Sn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在平面直角坐标系中，定义d（P，Q）=|x1﹣x2|+|y1﹣y2|为两点P（x1，y1），Q（x2，y2）之间的“折线距离”，在这个定义下，给出下列命题：

    ①到原点的“折线距离”等于1的点的集合是一个圆；

    ②到原点的“折线距离”小于等于2的点构成的区域面积为8；

    ③到M（0，﹣2），N（0，2）两点的“折线距离”相等的点的轨迹方程是y=0；

    ④直线y=x+1上的点到N（0，2）的“折线距离”的最小值为1．

    其中真命题有（　　）

    　

    A．

    1个

    B．

    2个

    C．

    3个

    D．

    4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若实数成等比数列，非零实数分别为与，与的等差中项，则下列结论正确的是                                                          

    A．        B．      C．      D．

    查看答案和解析>>

    同步练习册答案