某同学在研究性学习中，收集到某制药厂车间工人数（单位：十人）与药品产量（单位：万盒）的数据如表所示：
| 工人数：x（单位：十人） | 1 | 2 | 3 | 4 |
| 药品产量：y（单位：万盒） | 3 | 4 | 5 | 6 |
（1）请画出如表数据的散点图；
（2）参考公式，根据表格提供的数据，用最小二乘法求出y关于x的线性回归方程y=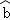
x+
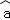；（参考数据
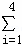i2=30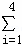，xiyi=50）
（3）试根据（2）求出的线性回归方程，预测该制药厂车间工人数为45时，药品产量是多少？
应用题天天练四川大学出版社系列答案科目：高中数学 来源： 题型：
下列说法中不正确的是（ ）
|
| A． | 对于线性回归方程 |
|
| B． | 茎叶图的优点在于它可以保存原始数据，并且可以随时记录 |
|
| C． | 将一组数据中的每一个数据都加上或减去同一常数后，方差恒不变 |
|
| D． | 掷一枚均匀硬币出现正面向上的概率是 |
查看答案和解析>>
科目：高中数学 来源： 题型：
在△ABC中，sinA：sinB：sinC=2：3：x，且△ABC为锐角三角形，则x的取值范围是（ ）
|
| A． |
| B． |
| C． | 2＜x＜ | D． |
|
查看答案和解析>>
科目：高中数学 来源： 题型：
设A（x1，f（x1）），B（x2，f（x2））是函数f（x）=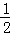
+log2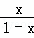
的图象上的任意两点．
（1）当x1+x2=1时，求f（x1）+f（x2）的值；
（2）设Sn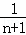=f（
）+f（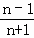
）+…+f（
）+f（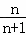
），其中n∈N*，求Sn；
（3）对于（2）中Sn，已知an=（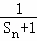
）2，其中n∈N*，设Tn为数列{an}的前n项的和，求证：
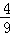≤Tn＜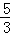
．
查看答案和解析>>
科目：高中数学 来源： 题型：
已知函数f（x）=ax2﹣4x+c（a，c∈R），满足f（2）=9，f（c）＜a，且函数f（x）的值域为[0，+∞）．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）设函数g（x）=
（k∈R），对任意x∈[1，2]，存在x0∈[﹣1，1]，使得g（x）＜f（x0）求k的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
某同学在研究性学习中，收集到某制药厂车间工人数（单位：十人）与药品产量（单位：万盒）的数据如表所示：
| 工人数：x（单位：十人） | 1 | 2 | 3 | 4 |
| 药品产量：y（单位：万盒） | 3 | 4 | 5 | 6 |
（1）请画出如表数据的散点图；
（2）参考公式，根据表格提供的数据，用最小二乘法求出y关于x的线性回归方程y=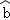
x+
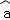；（参考数据
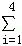i2=30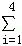，xiyi=50）
（3）试根据（2）求出的线性回归方程，预测该制药厂车间工人数为45时，药品产量是多少？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
=
x+
，直线必经过点（
，
）
，那么一枚硬币投掷2次一定出现正面
＜x＜5
，则2x+y的最大值是（ ）