
 如图,一圆形花圃内有5块区域,现有4中不同颜色的花,从4种花中选出若干种植入花蒲中,要求相邻两区域不同色,种法有( )
如图,一圆形花圃内有5块区域,现有4中不同颜色的花,从4种花中选出若干种植入花蒲中,要求相邻两区域不同色,种法有( )| A. | 324种 | B. | 216种 | C. | 244种 | D. | 240种 |
分析 若1,4同色,若1,4不同,2,4,若1,4不同,2,4不同相同三类,类中再分步,根据分步原理与分类原理计算出结果即可.
解答 解:若1,4同色,则1,4有四种种法,2,5各有三种种法,3有两种种法,故有4×3×3×2=72种,
若1,4不同,2,4相同,则1有四种种法,2,4有三种种法,3有三种种法,5有两种种法,故有4×3×3×2=72种,
若1,4不同,2,4不同,则1有四种种法,4有三种种法,2有两种种法,3有两种种法,5有两种种法,故有4×3×2×2×2=96种,
根据分类计数原理得种法有72+72+96=240
故选:D.
点评 本题考查计数原理的应用,考查分类讨论思想,避免重复和遗漏情况,是中档题


科目:高中数学 来源: 题型:解答题
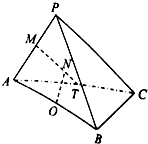 如图,在三棱锥P-ABC中,△PAC和△PBC均是边长为$\sqrt{2}$的等边三角形,AB=2,O,M,T分别是AB,PA,AC的中点.
如图,在三棱锥P-ABC中,△PAC和△PBC均是边长为$\sqrt{2}$的等边三角形,AB=2,O,M,T分别是AB,PA,AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{2}$ | C. | 10 | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在三棱柱ABC-A1B1C1中,各个侧面均是边长为2的正方形,D为线段AC的中点.
如图,在三棱柱ABC-A1B1C1中,各个侧面均是边长为2的正方形,D为线段AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com