
| A. | 15 | B. | 30 | C. | 31 | D. | 64 |
科目:高中数学 来源:2015-2016学年江苏泰兴中学高一下学期期中数学试卷(解析版) 题型:解答题
如图,经过村庄 有两条夹角为
有两条夹角为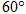 的公路
的公路 ,根据规划拟在两条公路之间的区域内建一工厂
,根据规划拟在两条公路之间的区域内建一工厂 ,分别在两条公路边上建两个仓库
,分别在两条公路边上建两个仓库 、
、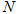 (异于村庄
(异于村庄 ),要求
),要求 (单位:千米).
(单位:千米).

(1)设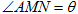 ,试写出
,试写出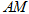 关于
关于 的表达式;
的表达式;
(2)如何设计,使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-1)2+(y-1)2=1 | B. | (x-1)2+(y-2)2=4 | C. | x2+(y-2)2=5 | D. | x2+(y-1)2=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{2}$ | B. | $-\frac{2}{3}$ | C. | 6 | D. | -6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
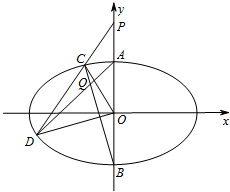 椭圆M:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的焦距为2$\sqrt{3}$,点P(0,2)关于直线y=-x的对称点在椭圆M上.
椭圆M:$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的焦距为2$\sqrt{3}$,点P(0,2)关于直线y=-x的对称点在椭圆M上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com