
分析 (1)过A作准线的垂线AA′垂足为A′,则AA′=4,AB=8,FK为△AA′B的中位线,于是p=FK=$\frac{1}{2}AA′$=2,借助几何图形求出斜率.
(2)设CD方程为y=$\sqrt{3}x+b$,联立方程组,求出直线PC与PD的斜率,令方程kPC•kPD=-4有解得△≥0,即可解出b的范围.
解答 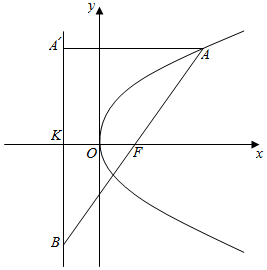 解:(1)过A作准线的垂线AA′垂足为A′,设准线交x轴与K点,则F($\frac{p}{2}$,0),K(-$\frac{p}{2}$,0)
解:(1)过A作准线的垂线AA′垂足为A′,设准线交x轴与K点,则F($\frac{p}{2}$,0),K(-$\frac{p}{2}$,0)
则AA′=AF=4,AB=2AF=8,A′B=$\sqrt{A{B}^{2}-AA{′}^{2}}$=4$\sqrt{3}$.
∵FK∥AA′,F是AB的中点,
∴FK=$\frac{1}{2}$AA′=2,即p=2.
∴抛物线方程为y2=4x.′
直线l的斜率k=$\frac{A′B}{AA′}$=$\sqrt{3}$.
(2)设直线CD的方程为y=$\sqrt{3}$x+b.
联立方程组$\left\{\begin{array}{l}{y=\sqrt{3}x+b}\\{{y}^{2}=4x}\end{array}\right.$,消元得:y2-$\frac{4y}{\sqrt{3}}$+$\frac{4b}{\sqrt{3}}$=0.
∴△=$\frac{16}{3}$-$\frac{16b}{\sqrt{3}}$>0,解得b<$\frac{\sqrt{3}}{3}$.
设C($\frac{{{y}_{1}}^{2}}{4}$,y1),D($\frac{{{y}_{2}}^{2}}{4}$,y2),P($\frac{{y}^{2}}{4}$,y).
则y1+y2=$\frac{4}{\sqrt{3}}$,y1y2=$\frac{4b}{\sqrt{3}}$.
∴kPC=$\frac{y-{y}_{1}}{\frac{{y}^{2}-{{y}_{1}}^{2}}{4}}$=$\frac{4}{y+{y}_{1}}$,kPD=$\frac{y-{y}_{2}}{\frac{{y}^{2}-{{y}_{2}}^{2}}{4}}$=$\frac{4}{y+{y}_{2}}$.
∵抛物线上存在一点P,使得直线PC与PD的斜率之积为-4,
∴$\frac{4}{y+{y}_{1}}$•$\frac{4}{y+{y}_{2}}$=-4有解.即y2+$\frac{4y}{\sqrt{3}}$+$\frac{4b}{\sqrt{3}}$+4=0有解.
∴△=$\frac{16}{3}$-$\frac{16b}{\sqrt{3}}$-14≥0,解得b≤-$\frac{13\sqrt{3}}{8}$.
∴直线CD在y轴上截距的最大值为-$\frac{13\sqrt{3}}{8}$.
点评 本题考查了抛物线的性质,直线与抛物线的位置关系,属于中档题.


科目:高中数学 来源:2016-2017学年广东清远三中高二上学期月考一数学(文)试卷(解析版) 题型:选择题
如果一个几何体的三视图如图所示,主视图与左视图是边长为2的正三角形、俯视图轮廓为正方形,(单位:cm),则此几何体的侧面积是( )

A.
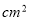 B.
B.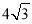
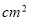
C.8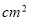 D.14
D.14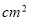
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{13}{18}$ | B. | $\frac{13}{22}$ | C. | $\frac{3}{22}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{3}$ | C. | 1 | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com