
| A. | (x-1)2+(y-1)2=1 | B. | (x-1)2+(y-2)2=4 | C. | x2+(y-2)2=5 | D. | x2+(y-1)2=2 |
分析 求得抛物线的焦点和准线方程,运用抛物线的定义可得△PMF为等腰三角形,P在MF上的投影为中点,由题意结合向量的投影概念,设出P的坐标,由两点的距离公式可得P的坐标,进而判断三角形的形状,求得圆心和半径,即可得到所求方程.
解答 解:抛物线C:y2=4x的焦点为F(1,0),准线方程为x=-1,
由抛物线的定义可得|PF|=|PM|,
即△PMF为等腰三角形,P在MF上的投影为中点,
由 $\overrightarrow{FP}$在$\overrightarrow{FM}$方向上的投影为$\sqrt{2}$,可得|MF|=2$\sqrt{2}$,
设P($\frac{{m}^{2}}{4}$,m),可得M(-1,m),
即有$\sqrt{{(1+1)}^{2}{+m}^{2}}$=2$\sqrt{2}$,
解得m=2,
即有P(1,2),M(-1,2),
三角形PFM为等腰直角三角形,∠MPF为直角,
三角形PFM的外接圆的圆心为MF的中点(0,1),
半径为$\sqrt{2}$,
可得圆的半径为x2+(y-1)2=2,
故选:D.
点评 本题考查抛物线的定义、方程和性质,向量的投影,圆的方程的求法,注意运用几何方法,考查化简整理的运算能力,属于中档题.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源:2015-2016学年江苏泰兴中学高一下学期期中数学试卷(解析版) 题型:填空题
如图,互不相同的点 和
和 分别在角
分别在角 的两条边上,所有
的两条边上,所有 相互平行,且所有梯形
相互平行,且所有梯形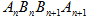 的面积均相等,设
的面积均相等,设 .若
.若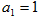 ,
, ,则数列
,则数列 的通项公式是
的通项公式是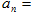 ____.
____.

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,5) | B. | (-∞,-1)∪(5,+∞) | C. | (-∞,1)∪(3,+∞) | D. | (1,3) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | [-1,+∞) | C. | (-∞,1] | D. | (-∞,-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com