
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
分析 运用A,B在抛物线上,满足抛物线方程,再由直线的斜率公式,化简整理计算即可得到所求值.
解答 解:由题意可得,y12=2x1,y22=2x2,
kAC=$\frac{{y}_{1}-0}{\frac{{y}_{1}^{2}}{2}-2}$,kBC=$\frac{{y}_{2}-0}{\frac{{y}_{2}^{2}}{2}-2}$,
若直线AC,BC的斜率互为相反数,
则kAC+kBC=0,$\frac{{y}_{1}}{{y}_{1}^{2}-4}+\frac{{y}_{2}}{{y}_{2}^{2}-4}=0$,
整理得:${y}_{1}{y}_{2}^{2}+{y}_{2}{y}_{1}^{2}-4{y}_{1}-4{y}_{2}=0$,
(y1y2-4)(y1+y2)=0,
由于y1y2>0,即y1y2=4.
故答案选:B.
点评 本题考查抛物线的方程和性质,主要考查抛物线的方程的运用,以及直线的斜率公式,考查化简整理的能力,属于中档题.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源:2017届四川巴中市高中高三毕业班10月零诊理数试卷(解析版) 题型:选择题
设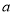 ,
,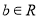 ,若
,若 :
: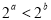 ,
,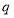 :
: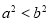 ,则
,则 是
是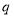 的( )
的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-1)2+(y-1)2=1 | B. | (x-1)2+(y-2)2=4 | C. | x2+(y-2)2=5 | D. | x2+(y-1)2=2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y2=12x | B. | y2=14x | C. | y2=16x | D. | y2=18x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | -1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
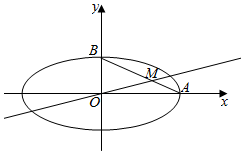 如图,椭圆E的方程为$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),点O为坐标原点,点A,B分别是椭圆的右顶点和上顶点,点M在线段AB上,满足BM=2MA,直线OM的斜率为$\frac{1}{4}$.
如图,椭圆E的方程为$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),点O为坐标原点,点A,B分别是椭圆的右顶点和上顶点,点M在线段AB上,满足BM=2MA,直线OM的斜率为$\frac{1}{4}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com