
 位学生(关心与不关心的各一半),
位学生(关心与不关心的各一半),
 ℅的把握认为是否关心创卫活动与性别有关?
℅的把握认为是否关心创卫活动与性别有关?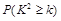 | 0.10 | 0.05 | 0.01 |
 | 2.706 | 3.841 | 6.635 |
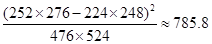
 ;
;| | 女 | 男 | 合计 |
| 关心 | | | 500 |
| 不关心 | | | 500 |
| 合计 | | 524 | 1000 |
| 参加活动次数 | 1 | 2 | 3 |
| 人数 | 10 | 50 | 40 |
 表示这两人参加活动次数之差的绝对值,求随机变量
表示这两人参加活动次数之差的绝对值,求随机变量 的分布列及数学期望
的分布列及数学期望 .
. ℅的把握认为是否关心创卫活动与性别有关.
℅的把握认为是否关心创卫活动与性别有关. 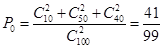
 | 0 | 1 | 2 |
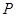 | 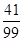 | 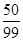 | 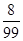 |
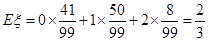 。
。| | 女 | 男 | 合计 |
| 关心 | 252 | 248 | 500 |
| 不关心 | 224 | 276 | 500 |
| 合计 | 476 | 524 | 1000 |
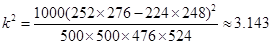
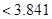 4分
4分 ℅的把握认为是否关心创卫活动与性别有关. 5分
℅的把握认为是否关心创卫活动与性别有关. 5分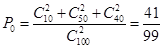 7分
7分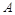 ,“这两人中一人参加2次活动,另一个参加3次活动”为事件
,“这两人中一人参加2次活动,另一个参加3次活动”为事件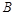 ,“这两人中一人参加1次活动,另一个参加两次活动”, “这两人中一人参加1次活动,另一个参加3次活动”为事件
,“这两人中一人参加1次活动,另一个参加两次活动”, “这两人中一人参加1次活动,另一个参加3次活动”为事件 . 8分
. 8分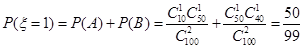 9分
9分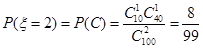 10分
10分 | 0 | 1 | 2 |
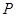 | 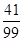 | 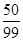 | 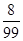 |
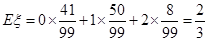 12分
12分

科目:高中数学 来源:不详 题型:解答题
 名男生和
名男生和 名女生进行了不记名的问卷调查,得到了如下的统计结果:
名女生进行了不记名的问卷调查,得到了如下的统计结果:| 上网时间(分钟) |  |  |  |  |  |
| 人数 | 5 | 25 | 30 | 25 | 15 |
| 上网时间(分钟) |  |  |  |  |  |
| 人数 | 10 | 20 | 40 | 20 | 10 |
 列联表,并回答能否有90%的把握认为“学生周日上网时间与性别有关”?
列联表,并回答能否有90%的把握认为“学生周日上网时间与性别有关”?| | 上网时间少于60分钟 | 上网时间不少于60分钟 | 合计 |
| 男生 | | | |
| 女生 | | | |
| 合计 | | | |
 ,其中
,其中
 | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 之间的几组数据如下表:
之间的几组数据如下表: | 1 | 2 | 3 | 4 | 5 | 6 |
 | 0 | 2 | 1 | 3 | 3 | 4 |

 求得的直线方程为
求得的直线方程为 则以下结论正确的是( )
则以下结论正确的是( ) B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 列联表:已知从全部210人中随机抽取1人为优秀的概率为
列联表:已知从全部210人中随机抽取1人为优秀的概率为 .
.| | 优秀 | 非优秀 | 总计 |
| 甲班 | 20 | | |
| 乙班 | | 60 | |
| 合计 | | | 210 |
 列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;
列联表,并判断若按99%的可靠性要求,能否认为“成绩与班级有关”;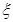 ,若每次抽取的结果是相互独立的,求
,若每次抽取的结果是相互独立的,求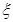 的分布列及数学期望
的分布列及数学期望 .
.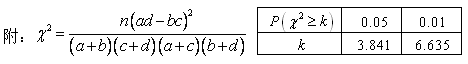
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 联表:
联表:| | 优秀 | 非优秀 | 合计 |
| 甲班 | 30 | | |
| 乙班 | | 50 | |
| 合计 | | | 200 |

 联表;
联表; 的把握认为“成绩与班级有关系”
的把握认为“成绩与班级有关系” ,若每次抽取得结果是相互独立的,求
,若每次抽取得结果是相互独立的,求 的分布列,期望
的分布列,期望 和方差
和方差


查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 列联表算得
列联表算得 的观测值
的观测值 ,参照附表:
,参照附表: | 0.050 | 0.010 | 0.001 |
 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,其中甲社区有驾驶员96人.若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12,21,25,43,则这四个社区驾驶员的总人数
,其中甲社区有驾驶员96人.若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12,21,25,43,则这四个社区驾驶员的总人数 为( )
为( )| A.920 | B.960 | C.808 | D.1200 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com