练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    回归直线方程为，则时，的估计值为              
    42.6

    试题分析：根据给定的线性回归方程可知，回归直线方程为，则时，则有的估计值为57.5-14.9=42.6 ，故答案为42.6。
    点评：根据回归方程将x代入可知y的预报值，属于基础题。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：单选题

    某校共有学生2000名，各年级男、女生人数如下表．已知在全校 学生中随机抽取1名，抽到二年级女生的概率是0．19．现用分层抽样的方法在全校抽取64名学生，则应在三年级抽取的学生人数为           ．
     
    		一年级
    		二年级
    		三年级
    女生
    		373


    男生
    		377
    		370

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某中学号召本校学生在本学期参加市创办卫生城的相关活动，学校团委对该校学生是否关心创卫活动用简单抽样方法调查了位学生（关心与不关心的各一半），
    结果用二维等高条形图表示，如图．

    （1）完成列联表，并判断能否有℅的把握认为是否关心创卫活动与性别有关？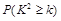

    		0.10
    		0.05
    		0.01

    		2.706
    		3.841
    		6.635
    （参考数据与公式：
    ；
     
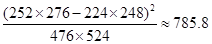
    		女
    		男
    		合计
    关心
    		 
    		 
    		500
    不关心
    		 
    		 
    		500
    合计
    		 
    		524
    		1000
     
    （2）已知校团委有青年志愿者100名，他们已参加活动的情况记录如下：
    参加活动次数
    		1
    		2
    		3
    人数
    		10
    		50
    		40
     
    （i）从志愿者中任选两名学生，求他们参加活动次数恰好相等的概率；
    （ii）从志愿者中任选两名学生，用表示这两人参加活动次数之差的绝对值，求随机变量的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    为调查某地区大学生是否爱好某项体育运动，用简单随机抽样方法从该地区的大学里调查了500位大学生，结果如下：
     
    		男
    		女
    爱好
    		40
    		30
    不爱好
    		160
    		270
    （1）  估计该地区大学生中，爱好该项运动的大学生的比例；
    （2）  能否有99％的把握认为该地区的大学生是否爱好该项体育运动与性别有关？
    附：

    		0．050
    		0．010
    		0．001

    		3．841
    		6．635
    		10．828

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    在对人们的休闲方式的一次调查中，共调查了人，其中女性人，男性人．女性中有人主要的休闲方式是看电视，另外人主要的休闲方式是运动；男性中有人主要的休闲方式是看电视，另外人主要的休闲方式是运动．
    （1）根据以上数据建立一个的列联表；
    （2）判断性别与休闲方式是否有关系．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    设有一个回归方程为，变量增加一个单位时，则
    A．平均增加个单位 B．平均增加2个单位
    C．平均减少个单位D．平均减少2个单位

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知x与y之间的一组数据：
    x
    		0
    		1
    		2
    		3
    y
    		1
    		3
    		5
    		7
    则y与x的线性回归方程为=bx+a必过（     ）
    A．点　　      B．点        C．点　　      D．点

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    下图a是某市参加2012年高考的学生身高条形统计图，从左到右的各条形表示的学生人数依次记为A1、A2、…、Am [如A2表示身高（单位：cm）在[150，155]内的学生人数]。图b是统计图a中身高在一定范围内学生人数的一个算法流程图。现要统计身高在160～180cm（含160cm，不含180cm）的学生人数，那么在流程图中的判断框内应填写的条件是 （    ）
    A．<9B．<8C．<7 D．<6

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某校为了解学生的学科学习兴趣，对初高中学生做了一个喜欢数学和喜欢语文的抽样调查，随机抽取了名学生，相关的数据如下表所示：
     
    		数学
    		语文
    		总计
    初中



    高中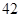



    总计



    (1) 用分层抽样的方法从喜欢语文的学生中随机抽取名，高中学生应该抽取几名?
    (2) 在(1)中抽取的名学生中任取名，求恰有名初中学生的概率．

    查看答案和解析>>

    同步练习册答案