
分析 当x=0时,y+z=13,y分别取0,1,2…,13时,z取13,12,…,0,有14个整数解;当x=1时,y+z=12,有13个整数解;…当x=13时,y+z=0,只有1组整数解,依此类推,然后把个数加起来即可.
解答 解:当x=0时,y+z=13,y分别取0,1,2…,13时,z取13,12,…,0,有14个整数解;
当x=1时,y+z=12,有13个整数解;
当x=2时,y+z=11,有12个整数解;
…
当x=13时,y+z=0,只有1组整数解,
故非负整数解的个数有14+13+…+3+2+1=105(个),
故答案为105.
点评 本题考查了三元一次不定方程的解,解题的关键是确定x、y、z的值,分类讨论.


科目:高中数学 来源: 题型:解答题
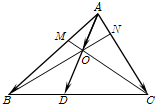 如图所示,在△ABC的边AB、AC上分别有点M、N,且AB=3AM,AC=4AN,BN与CM的交点是O,直线AO与BC交于点D.设$\overrightarrow{AB}=\overrightarrow m$,$\overrightarrow{AC}=\overrightarrow n$.
如图所示,在△ABC的边AB、AC上分别有点M、N,且AB=3AM,AC=4AN,BN与CM的交点是O,直线AO与BC交于点D.设$\overrightarrow{AB}=\overrightarrow m$,$\overrightarrow{AC}=\overrightarrow n$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | M∈a,a∈α | B. | M∈a,a?α | C. | M?a,a?α | D. | M?a,a∈α |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{e}{2}$ | B. | $\frac{\sqrt{e}}{2e}$ | C. | $\frac{2e}{3}$ | D. | e |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com