
分析 根据新定义,得出f(x)的周期,结合函数奇偶性的性质即可判断.
解答 解:①∵sin(x+π)=-sin(x)=sin(-x),
∴函数y=sinx具有“P(a)性质”;故①正确;
②∵若奇函数y=f(x)具有“P(2)性质”,
∴f(x+2)=f(-x)=-f(x),∴f(x)=f(2-x)=-f(x-2),
∴f(x+2)=f(x-2),
∴f(x)是周期为4的函数,
∴f(2015)=f(-1)=-f(1)=-1,故②不正确;
③∵若函数y=f(x)具有“P(4)性质”,
∴f(x+4)=f(-x),∴f(x+2)=f(2-x),
∴f(x)关于x=2对称,
∵图象关于点(1,0)成中心对称,
∴f(2-x)=-f(x),即f(2+x)=-f(-x),
又f(x+2)=f(2-x),∴f(x)=f(-x),
∴f(x)为偶函数,
∵图象关于点(1,0)成中心对称,且在(-1,0)上单调递减,
∴图象也关于点(-1,0)成中心对称,且在(-2,-1)上单调递减,
根据偶函数的对称得出:在(1,2)上单调递增;故③正确;
④∵f(x)具有“P(0)性质”和“P(3)性质”,
∴f(x)=f(-x),f(x+3)=f(-x)=f(x),
∴f(x)为偶函数,且周期为3,故④正确.
故答案为:①③④.
点评 本题考查了对新定义的理解与应用,函数周期性,奇偶性的性质,属于中档题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
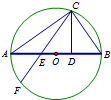 如图,AB是⊙O的直径,且AB=3,CD⊥AB于D,E为AD的中点,连接CE并延长交⊙O于F,若CD=$\sqrt{2}$,则EF=$\frac{{2\sqrt{3}}}{3}$.
如图,AB是⊙O的直径,且AB=3,CD⊥AB于D,E为AD的中点,连接CE并延长交⊙O于F,若CD=$\sqrt{2}$,则EF=$\frac{{2\sqrt{3}}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 是减函数 | B. | 是增函数或减函数 | ||
| C. | 是增函数 | D. | 未必是增函数或减函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com