
【题目】已知函数![]() ,若过点P(1,t)存在3条直线与曲线
,若过点P(1,t)存在3条直线与曲线![]() 相切,求t的取值范围__________。
相切,求t的取值范围__________。
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】某班共![]() 名同学,在一次数学考试中全班同学成绩全部介于
名同学,在一次数学考试中全班同学成绩全部介于![]() 分到
分到![]() 分之间.将成绩结果按如下方式分成五组:第一组
分之间.将成绩结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ,
, ![]() ,第五组
,第五组![]() .按上述分组方法得到的频率分布直方图如图所示,将成绩大于或等于
.按上述分组方法得到的频率分布直方图如图所示,将成绩大于或等于![]() 分且小于
分且小于![]() 分记为“良好”,
分记为“良好”, ![]() 分以上记为“优秀”,不超过分
分以上记为“优秀”,不超过分![]() 则记为“及格”.
则记为“及格”.
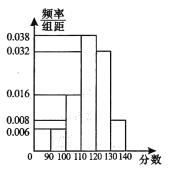
(1)求该班学生在这次数学考试中成绩“良好”的人数;
(2)若从第一、五组中共随机取出两个成绩,记![]() 为取得第一组成绩的个数,求
为取得第一组成绩的个数,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图四棱锥![]() 中,
中, ![]() 是梯形,AB∥CD,
是梯形,AB∥CD, ![]() ,AB=PD=4,CD=2,
,AB=PD=4,CD=2, ![]() ,M为CD的中点,N为PB上一点,且
,M为CD的中点,N为PB上一点,且![]() .
.
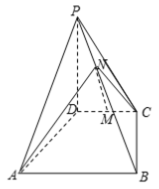
(1)若![]() MN∥平面PAD;
MN∥平面PAD;
(2)若直线AN与平面PBC所成角的正弦值为![]() ,求异面直线AD与直线CN所成角的余弦值。
,求异面直线AD与直线CN所成角的余弦值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
极坐标系的极点为直角坐标系![]() 的原点,极轴为
的原点,极轴为![]() 轴的正半轴,两神坐标系中的长度单位相同.已知曲线
轴的正半轴,两神坐标系中的长度单位相同.已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
, ![]() .
.
(Ⅰ)求曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)在曲线![]() 上求一点,使它到直线
上求一点,使它到直线![]() :
: 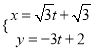 (
(![]() 为参数)的距离最短,写出
为参数)的距离最短,写出![]() 点的直角坐标.
点的直角坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com