
 如图,某旅游区拟建一主题游乐园,该游乐区为五边形区域ABCDE,其中三角形区域ABE为主题游乐区,四边形区域为BCDE为休闲游乐区,AB、BC,CD,DE,EA,BE为游乐园的主要道路(不考虑宽度).∠BCD=∠CDE=120°,∠BAE=60°,DE=3BC=3CD=3km.
如图,某旅游区拟建一主题游乐园,该游乐区为五边形区域ABCDE,其中三角形区域ABE为主题游乐区,四边形区域为BCDE为休闲游乐区,AB、BC,CD,DE,EA,BE为游乐园的主要道路(不考虑宽度).∠BCD=∠CDE=120°,∠BAE=60°,DE=3BC=3CD=3km.分析 (I)连接BD,由余弦定理可得BD,由已知可求∠CDB=∠CBD=30°,∠CDE=120°,可得∠BDE=90°,利用勾股定理即可得解BE的值.
(Ⅱ)设∠ABE=α,由正弦定理,可得AB=4sin(120°-α),AE=4sinα,利用三角函数恒等变换的应用化简可得AB+AE=4$\sqrt{3}$sin(α+30°),结合范围30°<α+30°<150°,利用正弦函数的性质可求AB+AE的最大值,从而得解.
解答 (本题满分为13分)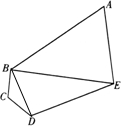 解:(I)如图,连接BD,在△BCD中,由余弦定理可得:BD2=BD2+CD2-2BC•CDcos∠BCD=1+1-2×1×1×(-$\frac{1}{2}$)=3,
解:(I)如图,连接BD,在△BCD中,由余弦定理可得:BD2=BD2+CD2-2BC•CDcos∠BCD=1+1-2×1×1×(-$\frac{1}{2}$)=3,
∴BD=$\sqrt{3}$,
∵BC=CD,
∴∠CDB=∠CBD=$\frac{180°-120°}{2}$=30°,
又∵∠CDE=120°,
∴∠BDE=90°,
∴在Rt△BDE中,BE=$\sqrt{B{D}^{2}+D{E}^{2}}$=$\sqrt{3+9}$=2$\sqrt{3}$.…5分
(Ⅱ)设∠ABE=α,∵∠BAE=60°,∴∠AEB=120°-α,
在△ABE中,由正弦定理,可得:$\frac{AB}{sin∠AEB}=\frac{AE}{sin∠ABE}=\frac{BE}{sin∠BAE}$,
∵$\frac{BE}{sin∠BAE}=\frac{2\sqrt{3}}{sin60°}$=4,
∴AB=4sin(120°-α),AE=4sinα,
∴AB+AE=4sin(120°-α)+4sinα
=4($\frac{\sqrt{3}}{2}cosα+\frac{1}{2}sinα$)+4sinα
=2$\sqrt{3}$cosα+6sinα
=4$\sqrt{3}$sin(α+30°),
∵0°<α<120°,
∴30°<α+30°<150°,
∴当α+30°=90°,即α=60°时,AB+AE取得最大值4$\sqrt{3}$km,即道路AB,AE长度之和的最大值为4$\sqrt{3}$km.…13分
点评 本题考查余弦定理,考查正弦定理,考查三角函数的化简,考查学生分析解决问题的能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题“若x>y,则x>|y|”的逆命题 | B. | 命题“若x2≤1,则x≤1”的否命题 | ||
| C. | 命题“若x=1,则x2-x=0”的否命题 | D. | 命题“若$a>b,则\frac{1}{a}<\frac{1}{b}$”的逆否命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com