
数列 的通项公式为
的通项公式为 ,等比数列
,等比数列 满足
满足 .
.
(1)求数列 的通项公式;
的通项公式;
(2)求数列 的前
的前 项和
项和 ;
;
(3)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
(1) ; (2)
; (2)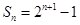 ;(3)
;(3)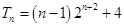
解析试题分析:(1)求等比数列通项,一般方法为待定系数法,设公比为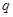 ,利用条件
,利用条件 列出关于
列出关于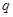 的方程:
的方程: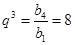 ,
,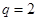 ,代入通项公式即可:
,代入通项公式即可: ;(2)利用等比数列前
;(2)利用等比数列前 项和
项和 公式:
公式: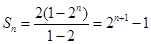 ;注意代公式时的前提条件;
;注意代公式时的前提条件; ,而而
,而而 时,
时,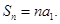 (3)数列
(3)数列 通项为“等比乘等差”型,所以求和用“错位相减法”, 令
通项为“等比乘等差”型,所以求和用“错位相减法”, 令 ,则
,则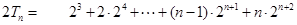 ,两式相减得
,两式相减得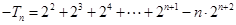
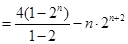 所以,
所以,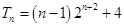 ,用“错位相减法”求和很容易出错,须注意三个方面,一是两式相减时,项的符号变化,二是中间求和时,须明确项的个数,三是最后须除以
,用“错位相减法”求和很容易出错,须注意三个方面,一是两式相减时,项的符号变化,二是中间求和时,须明确项的个数,三是最后须除以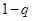 ,才可得到最后结果.
,才可得到最后结果.
试题解析:
(I)由已知,得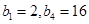 ,
,
且数列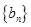 为等比数列,设公比为
为等比数列,设公比为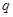 ,则
,则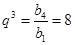 , 1分
, 1分
解得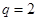 , 2分
, 2分
则数列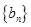 的通项公式为
的通项公式为 ; 3分
; 3分
(II)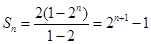 ; 6分
; 6分
(III)由已知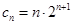 ,
,
所以,  . ① 7分
. ① 7分 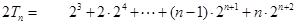 ②8分
②8分
①-②,得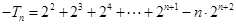 10分
10分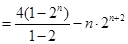
所以,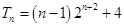 12分
12分
考点:等比数列通项及和项,错位相减法求和


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:高中数学 来源: 题型:解答题
某种平面分形图如下图所示,一级分形图是由一点出发的三条线段,长度均为1,两两夹角为 ;二级分形图是在一级分形图的每条线段的末端出发再生成两条长度为原来
;二级分形图是在一级分形图的每条线段的末端出发再生成两条长度为原来 的线段,且这两条线段与原线段两两夹角为
的线段,且这两条线段与原线段两两夹角为 ;依此规律得到
;依此规律得到 级分形图.
级分形图.
(1) 级分形图中共有 条线段;
级分形图中共有 条线段;
(2) 级分形图中所有线段长度之和为 .
级分形图中所有线段长度之和为 .
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某市为控制大气PM2.5的浓度,环境部门规定:该市每年的大气主要污染物排放总量不能超过55万吨,否则将采取紧急限排措施.已知该市2013年的大气主要污染物排放总量为40万吨,通过技术改造和倡导绿色低碳生活等措施,此后每年的原大气主要污染物排放最比上一年的排放总量减少10%.同时,因为经济发展和人口增加等因素,每年又新增加大气主要污染物排放量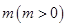 万吨.
万吨.
(1)从2014年起,该市每年大气主要污染物排放总量(万吨)依次构成数列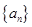 ,求相邻两年主要污染物排放总量的关系式;
,求相邻两年主要污染物排放总量的关系式;
(2)证明:数列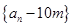 是等比数列;
是等比数列;
(3)若该市始终不需要采取紧急限排措施,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
等比数列{an}中,a1,a2,a3分别是下表第一、二、三行中的某一个数,且a1,a2,a3中的任何两个数不在下表的同一列.
(1)求数列{an}的通项公式;
(2)若数列{bn}满足:bn=an+(-1)nlnan,求数列{bn}的前n项和Sn·
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
学校餐厅每天供应500名学生用餐,每星期一有A, B两种菜可供选择。调查表明,凡是在这星期一选A菜的,下星期一会有 改选B菜;而选B菜的,下星期一会有
改选B菜;而选B菜的,下星期一会有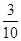 改选A菜。用
改选A菜。用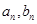 分别表示第
分别表示第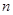 个星期选A的人数和选B的人数.
个星期选A的人数和选B的人数.
⑴试用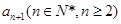 表示
表示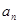 ,判断数列
,判断数列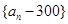 是否成等比数列并说明理由;
是否成等比数列并说明理由;
⑵若第一个星期一选A种菜的有200人,那么第10个星期一选A种菜的大约有多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
我们把一系列向量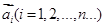 排成一列,称为向量列,记作
排成一列,称为向量列,记作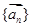 ,又设
,又设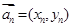 ,假设向量列
,假设向量列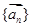 满足:
满足: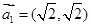 ,
,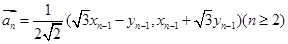 。
。
(1)证明数列 是等比数列;
是等比数列;
(2)设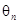 表示向量
表示向量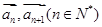 间的夹角,若
间的夹角,若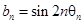 ,记
,记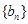 的前
的前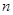 项和为
项和为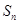 ,求
,求 ;
;
(3)设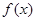 是
是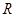 上不恒为零的函数,且对任意的
上不恒为零的函数,且对任意的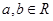 ,都有
,都有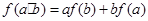 ,若
,若 ,
,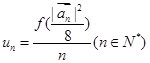 ,求数列
,求数列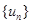 的前
的前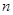 项和
项和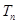 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在各项均为正数的等比数列{an}中,已知a2=2a1+3,且3a2,a4,5a3成等差数列.
(1)求数列{an}的通项公式;
(2)设bn=log3an,求数列{anbn}的前n项和Sn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com