
【题目】设函数![]() ,
, ![]() (
(![]() ).
).
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若函数![]() 在
在![]() 处取得极大值,求正实数
处取得极大值,求正实数![]() 的取值范围.
的取值范围.
【答案】(I)详见解析;(II)![]() .
.
【解析】试题分析:
(1)首先求得函数的导函数,然后结合参数分类讨论,
当![]() 时,
时, ![]() 的单调增区间为
的单调增区间为![]() ;
;
当![]() 时,
时, ![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
(2)求解![]() 的导函数,结合
的导函数,结合![]() 的结论分类讨论可得正实数
的结论分类讨论可得正实数![]() 的取值范围为
的取值范围为![]() .
.
试题解析:(Ⅰ)由![]() ,
, ![]() ,
,
所以![]() .
.
当![]() ,
, ![]() 时,
时, ![]() ,函数
,函数![]() 在
在![]() 上单调递增;
上单调递增;
当![]() ,
, ![]() 时,
时, ![]() ,函数
,函数![]() 单调递增,
单调递增, ![]() 时,
时, ![]() ,函数
,函数![]() 单调递减.
单调递减.
所以当![]() 时,
时, ![]() 的单调增区间为
的单调增区间为![]() ;
;
当![]() 时,
时, ![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
(Ⅱ)因为![]() ,
,
所以![]() 且
且![]() .
.
由(Ⅰ)知①当![]() 时,
时, ![]() ,由(Ⅰ)知
,由(Ⅰ)知![]() 在
在![]() 内单调递增,可得当
内单调递增,可得当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() .
.
所以![]() 在
在![]() 内单调递减,在
内单调递减,在![]() 内单调递增,所以
内单调递增,所以![]() 在
在![]() 处取得极小值,不合题意.
处取得极小值,不合题意.
②当![]() 时,
时, ![]() ,
, ![]() 在
在![]() 内单调递增,在
内单调递增,在![]() 内单调递减,所以当
内单调递减,所以当![]() 时,
时, ![]() ,
, ![]() 单调递减,不合题意.
单调递减,不合题意.
③当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
, ![]() 单调递增,当
单调递增,当![]() 时,
时, ![]() ,
, ![]() 单调递减.
单调递减.
所以![]() 在
在![]() 处取极大值,符合题意.
处取极大值,符合题意.
综上可知,正实数![]() 的取值范围为
的取值范围为![]() .
.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知经过原点的直线与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 为椭圆上不同于
为椭圆上不同于![]() 的一点,直线
的一点,直线![]() 的斜率均存在,且直线
的斜率均存在,且直线![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求椭圆![]() 的离心率;
的离心率;
(2)若![]() ,设
,设![]() 分别为椭圆的左、右焦点,斜率为
分别为椭圆的左、右焦点,斜率为![]() 的直线
的直线![]() 经过椭圆的右焦点,且与椭圆交于
经过椭圆的右焦点,且与椭圆交于![]() 两点,若点
两点,若点![]() 在以
在以![]() 为直径的圆内部,求
为直径的圆内部,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() ),若椭圆
),若椭圆![]() 上的一动点到右焦点的最短距离为
上的一动点到右焦点的最短距离为![]() ,且右焦点到直线
,且右焦点到直线![]() 的距离等于短半轴的长,已知
的距离等于短半轴的长,已知![]() ,过
,过![]() 的直线与椭圆交于
的直线与椭圆交于![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设Sn是数列{an}的前n项和,且2an+Sn=An2+Bn+C.
(1)当A=B=0,C=1时,求an;
(2)若数列{an}为等差数列,且A=1,C=﹣2. ①设bn=2nan , 求数列{bn}的前n项和;
②设cn= ![]() ,若不等式cn≥
,若不等式cn≥ ![]() 对任意n∈N*恒成立,求实数m的取值范围.
对任意n∈N*恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某算法的程序图如图所示,其中输入的变量x在1,2,3,…,30这30个整数中等可能随机产生. 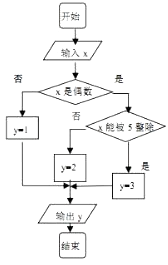
(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数,下面是甲、乙所作频数统计表的部分数据: 甲的频数统计表(部分)
运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
50 | 24 | 19 | 7 |
… | … | … | … |
2000 | 1027 | 776 | 197 |
乙的频数统计表(部分)
运行次数 | 输出y=1的频数 | 输出y=2的频数 | 输出y=3的频数 |
50 | 26 | 11 | 13 |
… | … | … | … |
2000 | 1051 | 396 | 553 |
当n=2000时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断甲、乙中谁所编写的程序符合算法要求的可能性较大.
查看答案和解析>>
科目:高中数学 来源: 题型:
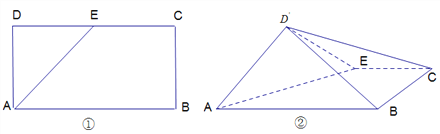
【题目】如图①,在矩形![]() 中,
中, ![]() ,
, ![]() 是
是![]() 的中点,将三角形
的中点,将三角形![]() 沿
沿![]() 翻折到图②的位置,使得平面
翻折到图②的位置,使得平面![]() 平面
平面![]() .
.
(Ⅰ)在线段![]() 上确定点
上确定点![]() ,使得
,使得![]() 平面
平面![]() ,并证明;
,并证明;
(Ⅱ)求![]() 与
与![]() 所在平面构成的锐二面角的正切值.
所在平面构成的锐二面角的正切值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com