
| A. | $\frac{{5\sqrt{3}}}{2}$ | B. | $\frac{{5\sqrt{21}}}{7}$ | C. | $\frac{{5\sqrt{7}}}{7}$ | D. | $\frac{{5\sqrt{2}}}{2}$ |
分析 根据平面向量投影的定义,计算$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$、$\overrightarrow{a}$$•\overrightarrow{b}$以及|$\overrightarrow{b}$|的值,代入投影公式计算即可.
解答 解:$|\overrightarrow{e_1}|=2$,$|\overrightarrow{e_2}|=1$,$\overrightarrow{e_1}$,$\overrightarrow{e_2}$的夹角为60°,
∴$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$=2×1×cos60°=1;
又$\vec a=2$$\overrightarrow{e_1}$+$\overrightarrow{e_2}$,$\vec b=\overrightarrow{e_1}+2\overrightarrow{e_2}$,
∴$\overrightarrow{a}$$•\overrightarrow{b}$=2${\overrightarrow{{e}_{1}}}^{2}$+5$\overrightarrow{{e}_{1}}$•$\overrightarrow{{e}_{2}}$+2${\overrightarrow{{e}_{2}}}^{2}$=2×22+5×1+2×12=15,
|$\overrightarrow{b}$|=$\sqrt{{(\overrightarrow{{e}_{1}}+2\overrightarrow{{e}_{2}})}^{2}}$=$\sqrt{{\overrightarrow{{e}_{1}}}^{2}+4\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}+{4\overrightarrow{{e}_{2}}}^{2}}$=$\sqrt{4+4×1+4×1}$=2$\sqrt{3}$,
∴$\vec a$在$\vec b$上的投影为|$\overrightarrow{a}$|cosθ=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{b}|}$=$\frac{15}{2\sqrt{3}}$=$\frac{5\sqrt{3}}{2}$.
故选:A.
点评 本题考查了平面向量投影的定义与应用问题,是基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
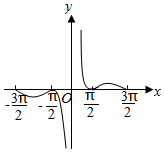 已知函数f(x)的图象如图所示,则f(x)的解析式可能是( )
已知函数f(x)的图象如图所示,则f(x)的解析式可能是( )| A. | $\frac{|cos3x|}{x}$ | B. | $\frac{1+cos2x}{2x}$ | ||
| C. | $\frac{(4{x}^{2}-{π}^{2})(4{x}^{2}-9{π}^{2})}{{x}^{5}}$ | D. | $\frac{|sin2x|}{x}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+3i | B. | 1+i | C. | 1-i | D. | 1-3i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,$\frac{1}{3}$] | B. | [-$\frac{1}{2}$,$\frac{1}{3}$] | C. | [-$\frac{1}{2}$,1) | D. | [-$\frac{1}{2}$,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com