
分析 (1)根据数量积的计算公式便可得出$cos<\overrightarrow{a},\overrightarrow{b}>=-\frac{\sqrt{2}}{2}$,这样即可得出$<\overrightarrow{a},\overrightarrow{b}>$的值;
(2)进行数量积的运算即可.
解答 解:(1)$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos<\overrightarrow{a},\overrightarrow{b}>=12cos<\overrightarrow{a},\overrightarrow{b}>=-6\sqrt{2}$;
∴$cos<\overrightarrow{a},\overrightarrow{b}>=-\frac{\sqrt{2}}{2}$;
∴$<\overrightarrow{a},\overrightarrow{b}>=\frac{3π}{4}$;
(2)$(2\overrightarrow{a}-\overrightarrow{b})•(\overrightarrow{a}+2\overrightarrow{b})$=$2{\overrightarrow{a}}^{2}+3\overrightarrow{a}•\overrightarrow{b}-2{\overrightarrow{b}}^{2}$
=$32-18\sqrt{2}-18$
=$14-18\sqrt{2}$.
点评 考查向量数量积的运算及其计算公式,已知三角函数求角.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(2,+∞) | B. | [1,2] | C. | [-1,1)∪(2,3] | D. | [-1,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
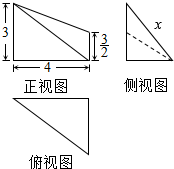 某几何体的三视图如图所示,若该几何体的体积为3$\sqrt{7}$,则侧视图中线段的长度x的值是( )
某几何体的三视图如图所示,若该几何体的体积为3$\sqrt{7}$,则侧视图中线段的长度x的值是( )| A. | 5 | B. | 4 | C. | 2$\sqrt{7}$ | D. | $\sqrt{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>0 | B. | 0<a≤1 | C. | a≥1 | D. | a≤1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
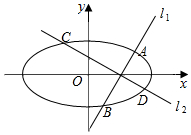 在平面直角坐标系中,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,F为椭圆的右焦点,过点F任作一条直线l1,交椭圆E于A,B两点,当l1垂直于x轴时,|AB|=1.
在平面直角坐标系中,已知椭圆E:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,F为椭圆的右焦点,过点F任作一条直线l1,交椭圆E于A,B两点,当l1垂直于x轴时,|AB|=1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com