练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    △ABC的边BC在平面 α内，A不在平面 α内，△ABC与α所成的角为θ（锐角），AA′⊥α，则下列结论中成立的是（　　）
    A、S△ABC=S△A′BC•cosθ
    B、S△A′BC=S△ABC•cosθ
    C、S△A′BC=S△ABC•sinθ
    D、S△ABC=S△A′BC•sinθ
    考点：二面角的平面角及求法
    专题：空间角
    分析：由已知得cosθ=
    S△A′BC
    S△ABC
    ，由此能求出S△A′BC=S△ABC•cosθ．
    解答： 解：∵△ABC的边BC在平面 α内，A不在平面 α内，
    △ABC与α所成的角为θ（锐角），AA′⊥α，
    ∴cosθ=
    S△A′BC
    S△ABC
    ，
    ∴S△A′BC=S△ABC•cosθ．
    故选：B．
    点评：本题考查命题真假的判断，是基础题，解题时要注意二面角的性质的合理运算．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    下列结论：①a=1是函数y=3sin（2ax+1）+2的周期为π的充要条件；②若“存在x0∈R，使得ax02+（a-3）x0+1≤0”是假命题，则1＜a＜9；③某人向一个圆内投镖，则镖扎到该圆的内接正三角形区域内的概率为
    3
    		3
    4π
    ．其中正确的是
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知sinθ=
    2
    3
    ，cosθ=-
    		5
    3
    ，则角2θ所在的象限为第
     
    象限．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知椭圆的两焦点F1，F2在x轴上，|F1F2|=4
    		2
    ，P为椭圆上一点，且|PF1|=
    7
    2
    ，|PF2|=
    5
    2
    ，则此椭圆的标准方程为（　　）
    A、
    x2
    3
    +y2=1
    B、x2+
    y2
    3
    =1
    C、
    x2
    9
    +y2=1
    D、x2+
    y2
    9
    =1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

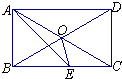    如图，矩形ABCD中，AE平分∠BAD交BC于E，∠CAE=15°，则以下结论：①△ODC是等边三角形；②BC=2AB；③∠AOE=135°；④S△AOE=S△COE，⑤∠AEO=30°其中正确的有（　　）
    A、1个B、2个C、3个D、4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知x+
    1
    x
    =-1，则x2014+
    1
    x2014
    的值为（　　）
    A、-1B、1C、2D、-2i

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知直线l：2x+3y+1=0被圆C：x2+y2=1所截得的弦长为d，则下列直线中被圆C截得的弦长同样为d的直线是（　　）
    A、2x+4y-1=0
    B、2x+3y-1=0
    C、4x+3y-1=0
    D、3x+2y=0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=
    x2-
    a
    x
    +2x，x≠0
    4，x=0
    ，若方程f（x）=4有三个不相等的实根，则a的取值构成的集合是（　　）
    A、{a|-
    16
    27
    ＜a＜8}
    B、{-
    16
    27
    ，8}
    C、{-
    16
    27
    ，0，8}
    D、{a|{a＞8或a＜-
    16
    27
    }

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    下列命题错误的是（　　）
    A、命题“若x2+y2=0，则x，y全为零”的否定是：“若x2+y2≠0，则x，y全不为零”
    B、对于命题p：?x∈R，使得x2+x+1＜0；则￢p：?x∈R，均有x2+x+1≥0
    C、命题“若m＞0，则方程x2+x-m=0有实根”的逆否命题为“若方程x2+x-m=0无实根，则m≤0
    D、“x=1”是“x2-3x+2=0”的充分不必要条件

    查看答案和解析>>

    同步练习册答案