
分析 先求出两本书随机给甲、乙、丙三人的所有情况,再求出甲拿到的书的数目分别是0,1,2的情况及其概率,进而即可得出数学期望.
解答 解:两本书随机给甲、乙、丙三人,共有32=9种情况.
则甲拿到的书的数目ξ的概率P(ξ=2)=$\frac{{C}_{2}^{2}}{9}$=$\frac{1}{9}$,P(ξ=1)=$\frac{{C}_{2}^{1}{C}_{2}^{1}}{9}$=$\frac{4}{9}$,
∴P(ξ=0)=1-P(ξ=2)-P(ξ=1)=$\frac{4}{9}$.
∴Eξ=0+1×$\frac{4}{0}$+2×$\frac{1}{9}$=$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 熟练掌握乘法原理、古典概型的概率计算公式、离散型随机变量的期望的计算公式是解题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若α∥β,m?α,n?β,则m∥n | |
| B. | 若m,n?α,m∥β,n∥β,则α∥β | |
| C. | m,n是异面直线,若m∥α,m∥β,n∥β,则α∥β | |
| D. | 若α∥β,m∥α,则m∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
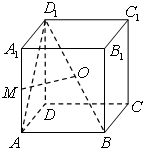 已知正方体ABCD-A1B1C1D1的棱长为1,点O是BD1的中点,M是棱AA1上的一点,请问:
已知正方体ABCD-A1B1C1D1的棱长为1,点O是BD1的中点,M是棱AA1上的一点,请问:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
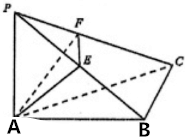 在三棱锥P-ABC中,已知PA⊥底面ABC,AB⊥BC,E,F分别是线段PB,PC上的动点.则下列说法错误的是( )
在三棱锥P-ABC中,已知PA⊥底面ABC,AB⊥BC,E,F分别是线段PB,PC上的动点.则下列说法错误的是( )| A. | 当AE⊥PB时,△AEF-定为直角三角形 | |
| B. | 当AF⊥PC时,△AEF-定为直角三角形 | |
| C. | 当EF∥平面ABC时,△AEF-定为直角三角形 | |
| D. | 当PC⊥平面AEF时,△AEF-定为直角三角形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com