
分析 (1)由题意知当AB⊥x轴时,直线AB的方程为:x=1,即m=0,从而A(1,$\frac{3}{2}$)或(1,-$\frac{3}{2}$).因为点A在抛物线上.所以$\frac{9}{4}$=2p,可得此时C2的焦点坐标,即可判断该焦点是否在直线AB上;
(2)由(1)知直线AB的斜率存在,故可设直线AB的方程为y=k(x-1),由$\left\{\begin{array}{l}{y=k(x-1)}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$消去y得(3+4k2)x2-8k2x+4k2-12=0.设A、B的坐标分别为(x1,y1),(x2,y2),联立直线方程和抛物线的方程,由根与系数的关系可推导出求出符合条件的k的值,即可得到所求直线方程.
解答 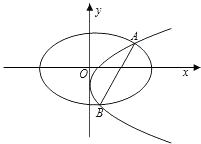 解:(1)当AB⊥x轴时,点A、B关于x轴对称,
解:(1)当AB⊥x轴时,点A、B关于x轴对称,
所以m=0,直线AB的方程为:x=1,
代入椭圆方程$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,
可得点A的坐标为(1,$\frac{3}{2}$)或(1,-$\frac{3}{2}$).
因为点A在抛物线上.
所以$\frac{9}{4}$=2p,即p=$\frac{9}{8}$.
即有抛物线的方程为y2=$\frac{9}{4}$x,
此时C2的焦点坐标为($\frac{9}{16}$,0),该焦点不在直线AB上;
(2)由(1)知直线AB的斜率存在,
故可设直线AB的方程为y=k(x-1).
由$\left\{\begin{array}{l}{y=k(x-1)}\\{3{x}^{2}+4{y}^{2}=12}\end{array}\right.$,消去y得(3+4k2)x2-8k2x+4k2-12=0①
设A、B的坐标分别为(x1,y1),(x2,y2),
则x1,x2是方程①的两根,x1+x2=$\frac{8{k}^{2}}{3+4{k}^{2}}$.
由$\left\{\begin{array}{l}{y=k(x-1)}\\{(y-m)^{2}=2px}\end{array}\right.$,
消去y得(kx-k-m)2=2px.②
因为C2的焦点F'($\frac{p}{2}$,m)在直线y=k(x-1)上,
所以m=k($\frac{p}{2}$-1),即m+k=$\frac{kp}{2}$.代入②有(kx-$\frac{kp}{2}$)2=2px.
即k2x2-p(k2+2)x+$\frac{{k}^{2}{p}^{2}}{4}$=0.③
由于x1,x2也是方程③的两根,
所以x1+x2=$\frac{p({k}^{2}+2)}{{k}^{2}}$,
从而$\frac{8{k}^{2}}{3+4{k}^{2}}$=$\frac{p({k}^{2}+2)}{{k}^{2}}$,
解得p=$\frac{8{k}^{4}}{(3+4{k}^{2})(2+{k}^{2})}$ ④
又AB过C1,C2的焦点,
所以|AB|=(x1+$\frac{p}{2}$)+(x2+$\frac{p}{2}$)=x1+x2+p=2-$\frac{1}{2}$x1+2-$\frac{1}{2}$x2,
则p=4-$\frac{3}{2}$(x1+x2)=4-$\frac{12{k}^{2}}{3+4{k}^{2}}$=$\frac{12+4{k}^{2}}{3+4{k}^{2}}$.⑤
由④、⑤式得$\frac{8{k}^{4}}{(3+4{k}^{2})(2+{k}^{2})}$=$\frac{12+4{k}^{2}}{3+4{k}^{2}}$,即k4-5k2-6=0.
解得k2=6.于是k=±$\sqrt{6}$.
则直线方程为y=±$\sqrt{6}$(x-1).
点评 本题考查直线和圆锥轴线的位置关系和综合运用,解题时要认真审题,仔细解答,注意公式的灵活运用.


科目:高中数学 来源: 题型:解答题
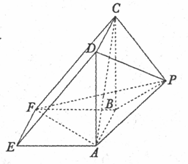 如图所示,该几何体是由一个直三棱柱ADE-BCF和一个正死棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2.
如图所示,该几何体是由一个直三棱柱ADE-BCF和一个正死棱锥P-ABCD组合而成,AD⊥AF,AE=AD=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 把一正方体沿对角面劈开,得一如图几何体,其中B1C1=A1C1=2,M为A1B1的中点,试作出过B1且与平面AMC1平行的截面,并计算该截面面积.
把一正方体沿对角面劈开,得一如图几何体,其中B1C1=A1C1=2,M为A1B1的中点,试作出过B1且与平面AMC1平行的截面,并计算该截面面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com