
分析 (1)欲求出切线方程,只须求出其斜率即可,故先利用导数求出在x=2处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决;
(2)函数f(x)在[1,2]上单调递增,f'(x)=3x2-2ax+1≥0在[1,2]上恒成立,可得2a≤3x+$\frac{1}{x}$在[1,2]上恒成立,求出右边的最小值,即可得出结论.
解答 解:(1)当a=1时,f(x)=x3-x2+x,
∴f′(x)=3x2-2x+1,
∴f′(2)=3×22-2×2+1=9,
∵f(2)=8-4+2=6,
∴曲线y=f(x)在点(2,f(2))处的切线方程y-6=9(x-2),即9x-y-12=0;
(2)∵函数f(x)在[1,2]上单调递增,
∴f'(x)=3x2-2ax+1≥0在[1,2]上恒成立,
∴2a≤3x+$\frac{1}{x}$在[1,2]上恒成立
令g(x)=3x+$\frac{1}{x}$,则g'(x)=$\frac{3{x}^{2}-1}{{x}^{2}}$>0,
∴g(x)=3x+$\frac{1}{x}$在1,2]上单调递增,
∴g(x)≥g(1)=4
∴2a≤4,
∴a≤2.
点评 本小题主要考查直线的斜率、导数的几何意义、利用导数研究曲线上某点切线方程、利用导数研究函数的单调性、恒成立问题的转换等基础知识,考查运算求解能力.属于中档题.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:选择题
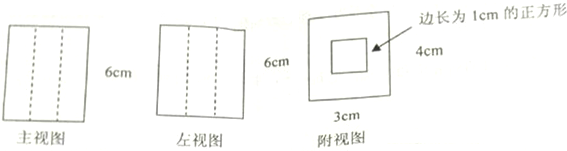
| A. | 中空的长方体,体积为72cm3 | B. | 中空的长方体,体积为66cm3 | ||
| C. | 实心长方体,体积为72cm3 | D. | 实心圆柱体,体积为66cm3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com