
分析 (1)由题意可知:求得切线方程,求得顶点坐标,求得a和b的值,求得椭圆C的标准方程;
(2)设A,B和C点坐标,分别将直线AP和BF的方程代入椭圆方程,利用韦达定理求得x1•x2和x2•x3,求得x2=x3,y2=-y1,由向量的数量积的坐标运算及二次函数的性质即可求得$\overrightarrow{PA}$•$\overrightarrow{FC}$的取值范围.
解答 解:(1)过点($\frac{6}{7}$,$\frac{4\sqrt{3}}{7}$)的切线方程为$\frac{6}{7}x$+$\frac{4\sqrt{3}}{7}$y=$\frac{12}{7}$,即3x+2$\sqrt{3}$y=6,
右顶点(2,0),上顶点(0,$\sqrt{3}$),
即a=2,b=$\sqrt{3}$,
椭圆C的标准方程$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)设A(x1,y1),B(x2,y2),C(x3,y3),
由题意知:AP的方程为y=k1(x-4),
$\left\{\begin{array}{l}{y={k}_{1}(x-4)}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,整理得:(4${k}_{1}^{2}$+3)x2+32${k}_{1}^{2}$+64${k}_{1}^{2}$-12=0,
x1•x2=$\frac{64{k}_{1}^{2}-12}{4{k}_{1}^{2}+3}$=16-$\frac{60}{4{k}_{1}^{2}+3}$,
将k1=$\frac{{y}_{2}}{{x}_{2}-4}$,${y}_{2}^{2}$=3-$\frac{3}{4}{x}_{2}^{2}$,代入得:x1•x2=$\frac{8{x}_{2}-5{x}_{2}^{2}}{5-2{x}_{2}}$,
BF的方程,y=k2(x-4),代入椭圆方程,
整理得:(4${k}_{2}^{2}$+3)x2-8${k}_{2}^{2}$x+4${k}_{2}^{2}$-12=0,
x2•x3=$\frac{4{k}_{2}^{2}-12}{4{k}_{2}^{2}+3}$=1-$\frac{15}{4{k}^{2}+3}$,
将k2=$\frac{{y}_{2}}{{x}_{2}-1}$,${y}_{2}^{2}$=3-$\frac{3}{4}$${x}_{2}^{2}$,代入得:x2•x3=$\frac{8{x}_{2}-5{x}_{2}^{2}}{5-2{x}_{2}}$,
∴x2=x3,
又AC不重合,
∴y2=-y1,
$\overrightarrow{PA}$•$\overrightarrow{FC}$=(x1-4,y1)•(x1-1,-y1),
=${x}_{1}^{2}$-5x1+4-${y}_{1}^{2}$,
=$\frac{7}{4}$${x}_{1}^{2}$-5x1+1,
=$\frac{7}{4}$(x1-$\frac{10}{7}$)2-$\frac{18}{7}$,(-2<x1<2),
∴-$\frac{18}{7}$≤$\overrightarrow{PA}$•$\overrightarrow{FC}$<18.
点评 本题考查了椭圆方程的求法,考查了直线与圆,圆与椭圆的位置关系,一元二次函数的性质,考查计算能力,属于中档题.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:选择题
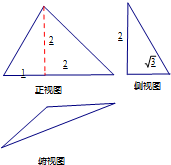
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | $\frac{5\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0.5 | C. | 2 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3×106 | B. | 3×105 | C. | 0.3×106 | D. | 30×104 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 是否需要志愿者 性别 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
| P(K2≥k) | 0.05 | 0.01 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com