
分析 由韦达定理可得b=-a,c=-6a,再讨论a>0,a<0,由二次不等式的解法,即可得到解集.
解答 解:ax2+bx+c=0的两个根为-2和3,
则-2+3=-$\frac{b}{a}$,-2×3=$\frac{c}{a}$,
即有b=-a,c=-6a,a≠0,
ax2-bx+c<0即为
ax2+ax-6a<0,a≠0,
当a>0时,x2+x-6<0,
(x+3)(x-2)<0,解得-3<x<2,
当a<0时,x2+x-6>0,
(x+3)(x-2)>0,解得x>2或x<-3.
综上可得,a>0时的解集为(-3,2);
a<0时的解集为(-∞,-3)∪(2,+∞).
点评 本题考查二次不等式的解法,注意对二次项系数的讨论,同时考查二次方程的韦达定理的运用,属于基础题和易错题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{22}}{14}$ | B. | $\frac{\sqrt{6}}{2}$ | C. | $\frac{3}{2}$ | D. | $\frac{3\sqrt{22}}{14}$或$\frac{\sqrt{6}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ax+by+cz | B. | az+by+cx | C. | ay+bz+cx | D. | ay+bx+cz |
查看答案和解析>>
科目:高中数学 来源:2016-2017学年安徽六安一中高二上文周末检测三数学试卷(解析版) 题型:选择题
若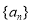 是等差数列,下列数列中仍为等差数列的有( )
是等差数列,下列数列中仍为等差数列的有( )
①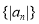 ;
;
②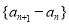 ;
;
③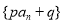 (
( ,
,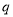 为常数);
为常数);
④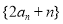 .
.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com