
【题目】下列四种说法
①在△ABC中,若∠A>∠B,则sinA>sinB;
②等差数列{an}中,a1 , a3 , a4成等比数列,则公比为![]() ;
;
③已知a>0,b>0,a+b=1,则![]() +
+![]() 的最小值为5+2
的最小值为5+2![]() ;
;
④在△ABC中,已知![]() =
=![]() =
=![]() , 则∠A=60°.
, 则∠A=60°.
正确的序号有
【答案】①③④
【解析】解:对于①在△ABC中,若∠A>∠B,则a>b,即有2RsinA>2RsinB,即sinA>sinB,则①正确;
对于②等差数列{an}中,a1 , a3 , a4成等比数列,则有a32=a1a4 , 即有(a1+2d)2=a1(a1+3d),
解得a1=﹣4d或d=0,则公比为![]() , 则②错误;
, 则②错误;
对于③,由于a>0,b>0,a+b=1,则![]()
当且仅当![]() b=
b=![]() a,取得最小值,且为5+2
a,取得最小值,且为5+2![]() , 则③正确;
, 则③正确;
对于④,在△ABC中,![]() 即tanA=tanB=tanC,
即tanA=tanB=tanC,
由于A,B,C为三角形的内角,则有A=B=C=60°,则④正确.
综上可得,正确的命题有①③④.
所以答案是:①③④.
【考点精析】解答此题的关键在于理解命题的真假判断与应用的相关知识,掌握两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知数列{an}满足a1=1,an+1=2an+1.
(1)求数列{an}的通项公式;
(2)令bn=![]() n(an+1),求数列{bn}的前n项和Tn .
n(an+1),求数列{bn}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C的一个焦点为![]() ,对应于这个焦点的准线方程为
,对应于这个焦点的准线方程为![]()
(1)写出抛物线![]() 的方程;
的方程;
(2)过![]() 点的直线与曲线
点的直线与曲线![]() 交于
交于![]() 两点,
两点,![]() 点为坐标原点,求
点为坐标原点,求![]() 重心
重心![]() 的轨迹方程;
的轨迹方程;
(3)点![]() 是抛物线
是抛物线![]() 上的动点,过点
上的动点,过点![]() 作圆
作圆![]() 的切线,切点分别是
的切线,切点分别是![]() .当
.当![]() 点在何处时,
点在何处时,![]() 的值最小?求出
的值最小?求出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:2x-y+6=0和直线l2:x=-1,F是抛物线C:y2=4x的焦点,点P在抛物线C上运动,当点P到直线l1和直线l2的距离之和最小时,直线PF被抛物线所截得的线段长是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的奇函数f(x)满足f(x+1)=f(﹣x),当x∈(0,1)时,f(x)=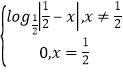 , 则f(x)在区间(1,
, 则f(x)在区间(1,![]() )内是( )
)内是( )
A.增函数且f(x)>0
B.增函数且f(x)<0
C.减函数且f(x)>0
D.减函数且f(x)<0
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=sin(x+![]() )(x∈R)的图象上所有点的纵坐标不变横坐标缩小到原来的
)(x∈R)的图象上所有点的纵坐标不变横坐标缩小到原来的![]() , 再把图象上各点向左平移
, 再把图象上各点向左平移![]() 个单位长度,则所得的图象的解析式为( )
个单位长度,则所得的图象的解析式为( )
A.y=sin(2x+![]() )
)
B.y=sin(![]() x+
x+![]() )
)
C.y=sin(2x+![]() )
)
D.y=sin(![]() x+
x+![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xoy中,已知圆C1:(x+3)2+(y﹣1)2=4和圆C2:(x﹣4)2+(y﹣5)2=4
若直线l过点A(4,0),且被圆C1截得的弦长为2![]() , 求直线l的方程
, 求直线l的方程
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)同时满足以下三个性质;①f(x)的最小正周期为π;②对任意的x∈R,都有f(x﹣ ![]() )=f(﹣x);③f(x)在(
)=f(﹣x);③f(x)在( ![]() ,
, ![]() )上是减函数.则f(x)的解析式可能是( )
)上是减函数.则f(x)的解析式可能是( )
A.f(x)=cos(x+ ![]() )
)
B.f(x)=sin2x﹣cos2x
C.f(x)=sinxcosx
D.f(x)=sin2x+cos2x
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知三棱锥P﹣ABC,PA⊥平面ABC,∠ACB=90°,∠BAC=60°,PA=AC,M为PB的中点. 
(Ⅰ)求证:PC⊥BC.
(Ⅱ)求二面角M﹣AC﹣B的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com