
已知箱中共有6个球,其中红球、黄球、蓝球各2个.每次从该箱中取1个球 (有放回,每球取到的机会均等),共取三次.设事件A:“第一次取到的球和第二次取到的球颜色相同”,事件B:“三次取到的球颜色都相同”,则P(B|A)=( )
A. B.
B.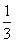 C.
C.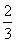 D.
D.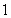
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
已知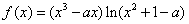 (
(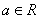 )
)
(Ⅰ)若方程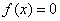 有3个不同的根,求实数
有3个不同的根,求实数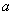 的取值范围;
的取值范围;
(Ⅱ)在(Ⅰ)的条件下,是否存在实数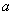 ,使得
,使得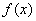 在
在 上恰有两个极值点
上恰有两个极值点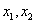 ,且满足
,且满足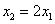 ,若存在,求实数
,若存在,求实数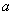 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数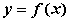 在(0,+
在(0,+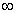 )内有定义,对于给定的正数K,定义函数
)内有定义,对于给定的正数K,定义函数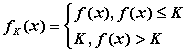 ,取函数
,取函数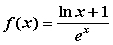 ,恒有
,恒有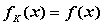 ,则
,则
A.K的最大值为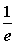 B.K的最小值为
B.K的最小值为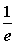 C.K的最大值为2 D.K的最小值为2
C.K的最大值为2 D.K的最小值为2
查看答案和解析>>
科目:高中数学 来源: 题型:
生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 | [70,76) | [76,82) | [82,88) | [88,94) | [94,100] |
| 元件A | 8 | 12 | 40 | 32 | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计元件A、元件B为正品的概率;
(2)生产一件元件A,若是正品可盈利50元,若是次品则亏损10元;生产一件元件B,若是正品可盈利100元,若是次品则亏损20元,在(1)的前提下,
(i)求生产5件元件B所获得的利润不少于300元的概率;
(ii)记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com