
圆C:x2+y2=1经过伸缩变换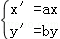 (其中a,b∈R,0<a<2,0<b<2,a、b的取值都是随机的.)得到曲线C′,则在已知曲线C′是焦点在x轴上的椭圆的情形下,C′的离心率
(其中a,b∈R,0<a<2,0<b<2,a、b的取值都是随机的.)得到曲线C′,则在已知曲线C′是焦点在x轴上的椭圆的情形下,C′的离心率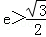 的概率等于 .
的概率等于 .
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 2.2矩阵乘法的性质练习卷(解析版) 题型:解答题
已知矩阵M=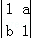 ,N=
,N=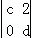 ,且MN=
,且MN=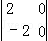 .
.
(Ⅰ)求实数a,b,c,d的值;
(Ⅱ)求直线y=3x在矩阵M所对应的线性变换下的像的方程.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.3线性变换的基本性质练习卷(解析版) 题型:选择题
(2011•上海模拟)关于x、y的二元线性方程组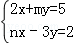 ,的增广矩阵经过变换,最后得到的矩阵为
,的增广矩阵经过变换,最后得到的矩阵为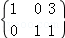 ,则 m+n=( )
,则 m+n=( )
A.﹣1 B.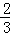 C.
C.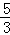 D.﹣
D.﹣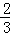
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.2二阶矩阵与平面向量的乘法(解析版) 题型:选择题
已知
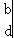 =ad﹣bc,则
=ad﹣bc,则 +
+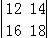 +…+
+…+ =( )
=( )
A.﹣2010 B.﹣2012 C.﹣2014 D.﹣2016
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.2二阶矩阵与平面向量的乘法(解析版) 题型:选择题
(2010•湛江一模)定义运算 =ad﹣bc,则函数
=ad﹣bc,则函数 图象的一条对称轴方程是( )
图象的一条对称轴方程是( )
A. B.
B.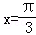 C.
C. D.
D.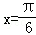
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷(解析版) 题型:填空题
直线y=3x绕原点逆时针旋转90°,再向右平移1个单位,所得到的直线为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-2 1.1线性变换与二阶矩阵练习卷(解析版) 题型:选择题
已知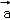 =(
=(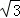 ,1),若将向量﹣2
,1),若将向量﹣2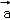 绕坐标原点逆时针旋转120°得到向量
绕坐标原点逆时针旋转120°得到向量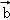 ,则
,则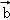 的坐标为( )
的坐标为( )
A.(0,4) B.(2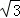 ,﹣2) C.(﹣2
,﹣2) C.(﹣2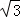 ,2) D.(2,﹣2
,2) D.(2,﹣2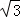 )
)
查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 3.3平面与圆锥面的截线练习卷(解析版) 题型:填空题
在空间中,取直线l为轴,直线l′与l相交于点O,其夹角为α(α为锐角),l′围绕l旋转得到以O为顶点,l′为母线的圆锥面,任取平面π,若它与轴l交角为β(π与l平行时,记β=0),则:当 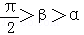 时,平面π与圆锥面的交线为 .
时,平面π与圆锥面的交线为 .

查看答案和解析>>
科目:高中数学 来源:[同步]2014年新人教A版选修4-1 2.4弦切角的性质练习卷(解析版) 题型:选择题
P在⊙O外,PC切⊙O于C,PAB交⊙O于A、B,则( )
A.∠PCB=∠B B.∠PAC=∠P C.∠PCA=∠B D.∠PAC=∠BCA
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com