

 ,AC=b,BC=a,运用类比方法探求空间中三棱锥的有关结论:
,AC=b,BC=a,运用类比方法探求空间中三棱锥的有关结论: ,给出空间中三棱锥的有关结论:________
,给出空间中三棱锥的有关结论:________科目:高中数学 来源:不详 题型:单选题
| A.一次三段论 | B.复合三段论 | C.不是三段论 | D.某个部分是三段论 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
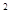 +y
+y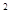 =a
=a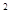 的面积S=
的面积S= a
a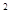 通过类比推理猜想椭圆
通过类比推理猜想椭圆 的面积S=
的面积S= ab. 之后利用演绎推理证明了这个公式是对的! 在平面直角坐标系中, 点集A="{" (x, y)|
ab. 之后利用演绎推理证明了这个公式是对的! 在平面直角坐标系中, 点集A="{" (x, y)|  }, 点集B="{(x," y)|
}, 点集B="{(x," y)|  , 则点集M="{(x," y)|x=x
, 则点集M="{(x," y)|x=x +x
+x , y=y
, y=y +y
+y , (x
, (x , y
, y )
) A, (x
A, (x , y
, y )
) B}所表示的区域的面积为_____________.
B}所表示的区域的面积为_____________. 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.没有一个内角是钝角 | B.有两个内角是钝角 |
| C.有三个内角是钝角 | D.至少有两个内角是钝角 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com